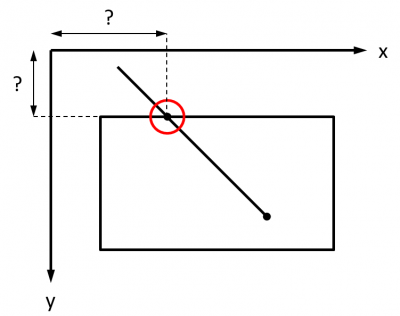
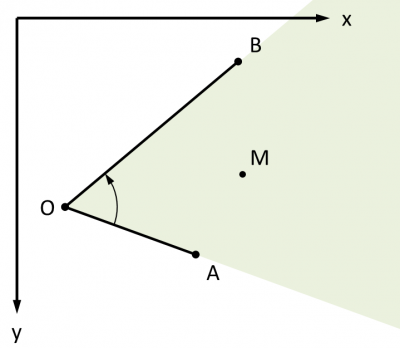
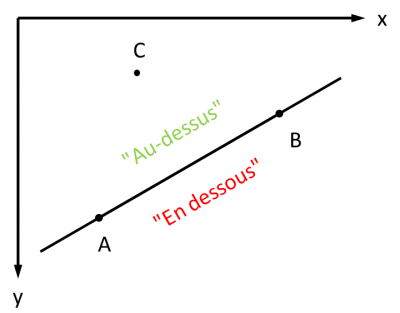
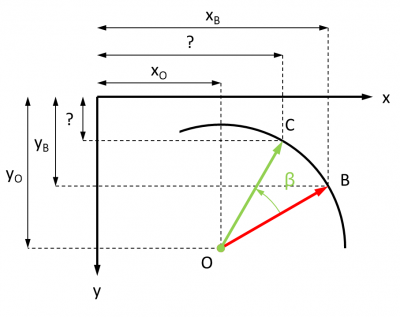
Comment déterminer l'intersection d'une demi-droite avec le périmètre d'un rectangle dans lequel l'origine de la demi-droite est situé, sans nécessairement que ce soit au centre de ce rectangle ?
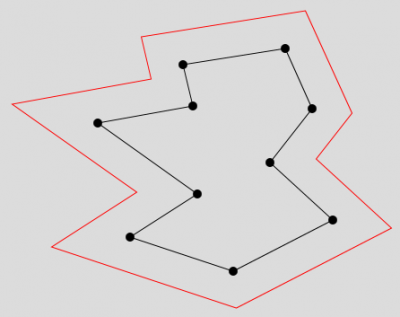
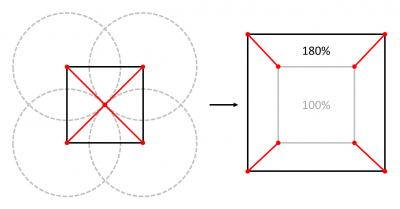
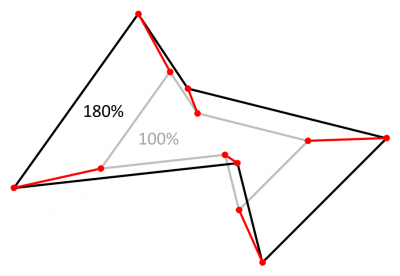
Ce problème de découpage (ou "clipping") est assez classique. Plus généralement, il se rencontre quand il s'agit de découper un polygone dès qu'il sort d'une surface de rendu, parce qu'il faut déterminer précisément les coordonnées des sommets résultant du découpage et/ou plus basiquement parce qu'il faut optimiser le rendu en le limitant à ce qui est visible.
Continuer la lecture de "Clipping de droite par un rectangle"