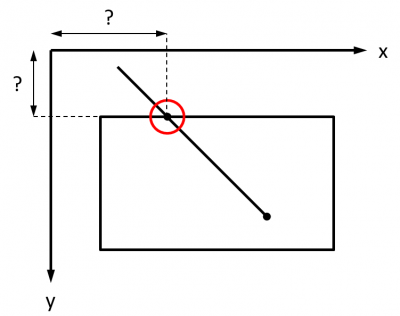
Comment déterminer l'intersection d'une demi-droite avec le périmètre d'un rectangle dans lequel l'origine de la demi-droite est situé, sans nécessairement que ce soit au centre de ce rectangle ?
Ce problème de découpage (ou "clipping") est assez classique. Plus généralement, il se rencontre quand il s'agit de découper un polygone dès qu'il sort d'une surface de rendu, parce qu'il faut déterminer précisément les coordonnées des sommets résultant du découpage et/ou plus basiquement parce qu'il faut optimiser le rendu en le limitant à ce qui est visible.
La solution
La solution passe par le recours un calcul d'intersection fondé sur les fonctions linéaires constituant les équations de la demi-droite et du côté qu'elle coupe.
Pour déterminer le côté en question, il faut diviser le rectangle en octants (ie : secteurs angulaires) centrés sur le point A d'origine de la demi-droite. Le côté est celui qui ferme l'octant dans lequel se trouve l'autre point B par lequel passe la demi-droite.
Le code JavaScript
En JavaScript, la solution se traduit par le code suivant :
/*------------------------------------------------------------------------------
Retourne les coordonnées du point d'intersection d'une demi-droite et d'un
rectangle dans lequel le point de départ de la demi-droite se trouve (repère X
de gauche à droite, Y de haut vers bas).
ENTREE :
xA, yA Point de départ de la demi-droite
xB, yB Point par lequel passe la demi-droite
x0, y0 Angle supérieur gauche du rectangle
x1, y1 Angle inférieur droit du rectangle
SORTIE :
x, y Point d'intersection {x, y}
------------------------------------------------------------------------------*/
function clipHalfLine (xA, yA, xB, yB, x0, y0, x1, y1) {
var xAB, yAB, x, y;
xAB = xB - xA;
yAB = yB - yA;
if (xAB < 0) {
if (yAB < 0) {
if ((xAB * (y0 - yA) - yAB * (x0 - xA)) > 0) {
x = x0;
y = ((x - xA) * yAB / xAB) + yA;
} else {
y = y0;
x = ((y - yA) * xAB / yAB) + xA;
}
}
else {
if ((xAB * (y1 - yA) - yAB * (x0 - xA)) < 0) {
x = x0;
y = ((x - xA) * yAB / xAB) + yA;
} else {
y = y1;
x = ((y - yA) * xAB / yAB) + xA;
}
}
}
else {
if (yAB < 0) {
if ((xAB * (y0 - yA) - yAB * (x1 - xA)) < 0) {
x = x1;
y = ((x - xA) * yAB / xAB) + yA;
} else {
y = y0;
x = ((y - yA) * xAB / yAB) + xA;
}
}
else {
if ((xAB * (y1 - yA) - yAB * (x1 - xA)) > 0) {
x = x1;
y = ((x - xA) * yAB / xAB) + yA;
} else {
y = y1;
x = ((y - yA) * xAB / yAB) + xA;
}
}
}
return ({x:x, y:y});
}
L'exemple
Cliquez ici pour accéder à une page de test minimaliste. Vous pourrez visualiser le code et le récupérer pour travailler avec.
Les maths
Le problème se résout donc en plusieurs temps. Tout d'abord, il faut déterminer l'équation de la demi-droite.
Calculer l'équation de la demi-droite
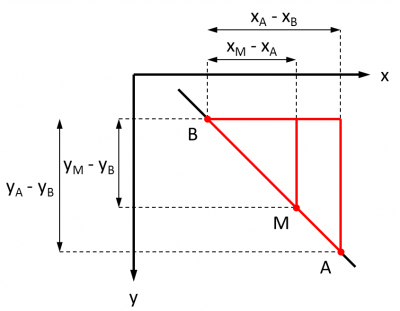
L'équation d'une droite passsant par deux points A et B prend la forme d'une fonction linéaire y = f (x). Cette équation permet très simplement de savoir si un point M appartient à la droite AB. En effet, si M est sur AB, alors yM = f (xM).
L'application du théorème de Thalès permet d'exprimer ainsi l'ordonnée d'un point de la droite en fonction de son ordonnée :
Ainsi :
(xM - xA) / (xA - xB) = (yM - yA) / (yA - yB)
D'où l'équation recherchée, qu'il est possible d'exprimer sous deux formes, la première permettant de déduire x de y, l'autre permettant de déduire y de x :
- yM = ((xM - xA) * (yA - yB) / (xA - xB)) + yA
- xM = ((yM - yA) * (xA - xB) / (yA - yB)) + xA
Les coordonnées de l'intersection de AB avec un côté du rectangle vérifient ces équations. Or, ces coordonnées sont déjà partiellement connues. En effet, si l'angle supérieur gauche du rectangle est le point (x0, y0) et l'angle inférieur droit est le point (x1, y1), alors :
| Bord | xM | yM |
| Haut | ((y0 - yA) * xBA / yBA) + xA | y0 |
| Bas | ((y1 - yA) * xBA / yBA) + xA | y1 |
| Gauche | x0 | ((x0 - xA) * yBA / xBA) + yA |
| Droit | x1 | ((x1 - xA) * yBA / xBA) + yA |
Avec :
- xBA = xA - xB
- yBA = yA - yB
Les coordonnées de l'intersection pouvant dorénavant être calculées, il reste à déterminer quelle intersection est la bonne.
Identifier la bonne intersection
Pour déterminer la bonne intersection, il faut parvenir à la qualifier par une combinaison unique de conditions. En l'espèce, cela conduit à :
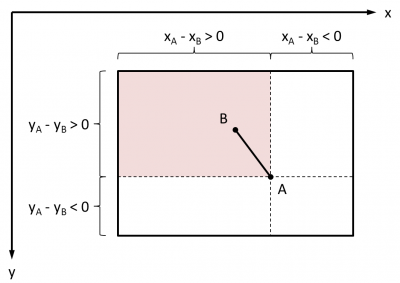
- déterminer le quadrant dans lequel se trouve l'intersection à partir de la combinaisons des signes de xBA et de yBA ;
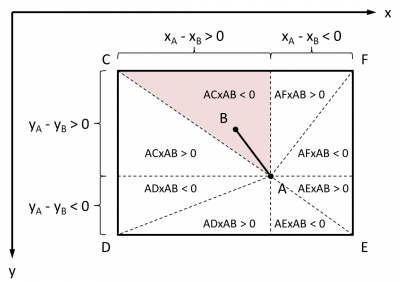
- déterminer l'octant du quadrant dans lequel se trouve l'intersection à partir de la position de B par rapport à la diagonale du quadrant passant par A.
En effet, le rectangle peut être décomposé en quatre secteurs droits, ou quadrants, qui chacun peut être divisé en deux secteurs, ou octants.
Comme il est possible de le constater, déterminer le bon quadrant est très simple. Il suffit de se baser sur la combinaison des signes de xBA et yBA :
Déterminer le bon octant dans le quadrant est plus délicat. B se trouve dans l'un ou l'autre octant du quadrant selon qu'il se trouve "au-dessus" ou "en-dessous" de la diagonale du quandrant passant par A.
Nous avons déjà vu comment déterminer la position d'un point par rapport à une droite. Il suffit donc d'appliquer cette solution :
Où il faut lire AFxAB comme le produit vectoriel des vecteurs AF (x0 - xA, y0 - yA) et AB (xB - xA, yB - yA), etc.
L'octant étant déterminé, le côté que la demi-droite coupe est déterminé. il n'y a plus qu'à calculer l'intersection à l'aide des formules données précédemment.