Comment déterminer les coordonnées de l'image d'un point par une rotation autour d'un autre point ?
La solution
La rotation d'un point B autour d'un point O peut être assimilée à une succession de rotations dans le repère de centre O :
- rotation d'un point A d'angle α autour de l'origine du repère d'origine O pour parvenir en B;
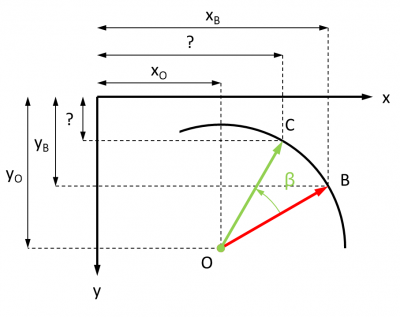
- rotation du point B d'angle β autour de l'origine du repère d'origine O pour parvenir en C.
Partant, il est possible d'appliquer les formules de combinaison de rotations dans un repère dont l'axe des abscisses est orienté de gauche à droite et dont l'axe des ordonnées est orienté du haut vers le bas.
Le code JavaScript
En JavaScript, la solution se traduit par le code suivant :
/*------------------------------------------------------------------------------
Retourne l'image d'un point par une rotation (repère X de gauche à droite, Y du
haut vers le bas).
ENTREE :
M Point à transformer
O Point centre de la rotation
angle Angle (en degrés)
SORTIE :
Image de M par la rotation d'angle angle autour de O (les coordonnées ne
sont pas entières).
------------------------------------------------------------------------------*/
function rotate (M, O, angle) {
var xM, yM, x, y;
angle *= Math.PI / 180;
xM = M.x - O.x;
yM = M.y - O.y;
x = xM * Math.cos (angle) + yM * Math.sin (angle) + O.x;
y = - xM * Math.sin (angle) + yM * Math.cos (angle) + O.y;
return ({x:Math.round (x), y:Math.round (y)});
}
L'exemple
Cliquez ici pour accéder à une page de test minimaliste qui utilise SVG. Vous pourrez visualiser le code et le récupérer pour travailler avec.
Les maths
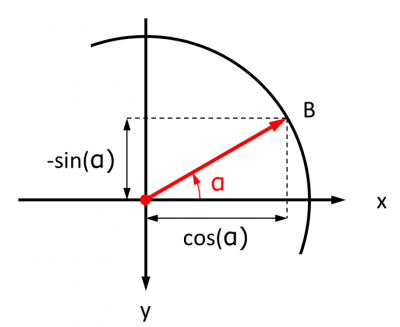
A la base, il faut considérer la situation à l'échelle du cercle trigonométrique, c'est-à-dire dans le repère dont l'origine est le centre d'un cercle de rayon 1, et où le sens de rotation d'un angle positif est à l'inverse du sens des aiguilles d'une montre (le sens trigonométrique) :
Dans ce repère, les coordonnées d'un point figurant sur le cercle sont par définition d'abscisse cos (α) et -sin (α) (noter le signe négatif, car l'axe des ordonnées est ici orienté vers le bas).
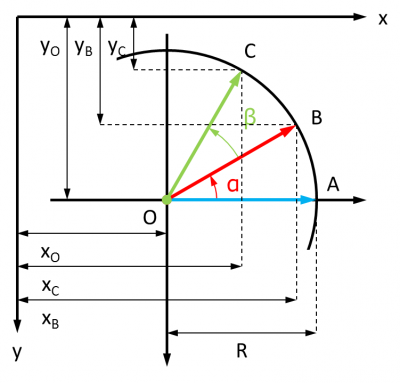
Ceci étant admis, il faut revenir à la situation initiale. Dans cette situation, le point B est l'image d'un point A par rotation d'angle α autour d'un point O. Dans le repère de centre O, ses coordonnées s'écrivent donc :
- xB - xO = R * cos (α)
- yB - yO = - R * sin (α)
Par ailleurs, le point C est l'image du point B par rotation d'angle β autour d'un point O. Ses coordonnées s'écrivent donc :
- xC = R * cos (α + β) + xO
- yC = - R * sin (α + β) + yO
Il faut ici appliquer des formules de décomposition du cosinus et du sinus :
- cos (α + β) = cos (α) * cos (β) - sin (α) * sin (β)
- sin (α + β) = cos (α) * sin (β) + sin (α) * cos (β)
Ce qui donne :
- xC = R * cos (α) * cos (β) - R * sin (α) * sin (β) + xO
- yC = - R * cos (α) * sin (β) - R * sin (α) * cos (β) + yO
Et donc :
- xC = (xB - xO) * cos (β) + (yB - yO) * sin (β) + xO
- yC = - (xB - xO) * sin (β) + (yB - yO) * cos (β) + yO