Comment déterminer si un point se trouve dans un secteur angulaire ?
La solution
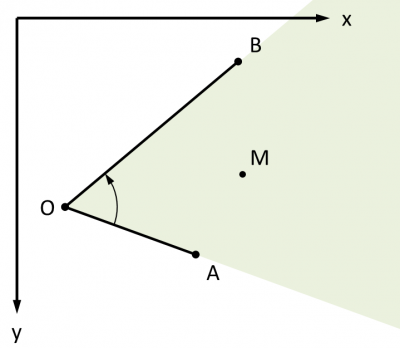
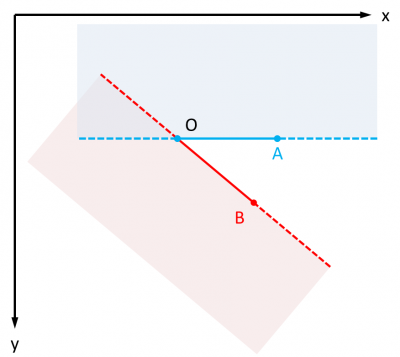
Si le point M se trouve dans le secteur angulaire défini AOB défini ainsi dans le sens de rotation trigonométrique (ie : l'angle résulte de la rotation de la droite OA autour de O dans le sens inverse des aiguilles d'une montre jusqu'à ce que cette droite soit confondue avec la droite OB), alors le point M se trouve dans le secteur si jamais il est "au-dessus" de OA et "en dessous" de OB.
Autrement dit, le problème se résume à comparer deux positions d'un point par rapport à une droite.
Le code JavaScript
En JavaScript, la solution se traduit par le code suivant :
/*------------------------------------------------------------------------------
Retourne un booléen indiquant si un point se trouve dans un secteur défini dans
le sens de rotation trigonométrique (repère X de gauche à droite, Y du haut vers
le bas).
ENTREE :
M Point dont la position est à tester
O Sommet du secteur
A Point de départ du secteur
B Point d'arrivée du secteur
SORTIE :
Booléen indiquant si le point est dans le secteur ou non.
------------------------------------------------------------------------------*/
function inSector (M, O, A, B) {
var cpAB, cpAM, cpBM;
cpAB = crossProduct ({x:(A.x - O.x), y:(A.y - O.y)}, {x:(B.x - O.x), y:(B.y - O.y)});
cpAM = crossProduct ({x:(A.x - O.x), y:(A.y - O.y)}, {x:(M.x - O.x), y:(M.y - O.y)});
cpBM = crossProduct ({x:(B.x - O.x), y:(B.y - O.y)}, {x:(M.x - O.x), y:(M.y - O.y)});
if (cpAB > 0) {
if ((cpAM > 0) && (cpBM < 0))
return (true);
else
return (false);
}
else {
if (!((cpAM < 0) && (cpBM > 0)))
return (true);
else
return (false);
}
}
Alternativement, le secteur pourrait être défini non pas par un sommet O et deux points A et B, mais par un sommet O, un point A et un angle de rotation de A autour de O.
/*------------------------------------------------------------------------------
Retourne un booléen indiquant si un point se trouve dans un secteur défini dans
le sens de rotation trigonométrique (repère X de gauche à droite, Y du haut vers
le bas).
ENTREE :
M Point dont la position est à tester
O Sommet du secteur
A Point de départ du secteur
AOB Angle de rotation de A autour de O dans le sens trigonométrique
définissant le secteur (en degrés et entre 0.0 et 360.0)
SORTIE :
Booléen indiquant si le point est dans le secteur ou non.
------------------------------------------------------------------------------*/
function inSector (M, O, A, AOB) {
var B, cpAM, cpBM;
B = {
x:O.x + (A.x - O.x) * Math.cos (AOB * Math.PI / 180.0) + (A.y - O.y) * Math.sin (AOB * Math.PI / 180.0),
y:O.y - (A.x - O.x) * Math.sin (AOB * Math.PI / 180.0) + (A.y - O.y) * Math.cos (AOB * Math.PI / 180.0)
};
cpAM = crossProduct ({x:(A.x - O.x), y:(A.y - O.y)}, {x:(M.x - O.x), y:(M.y - O.y)});
cpBM = crossProduct ({x:(B.x - O.x), y:(B.y - O.y)}, {x:(M.x - O.x), y:(M.y - O.y)});
if (AOB < 180.0) {
if ((cpAM > 0) && (cpBM < 0))
return (true);
else
return (false);
}
else {
if (!((cpAM < 0) && (cpBM > 0)))
return (true);
else
return (false);
}
}
L'exemple
Cliquez ici pour accéder à une page de test minimaliste. Vous pourrez visualiser le code et le récupérer pour travailler avec.
Pouvoir déterminer la position d'un point dans un secteur peut être fort utile en de nombreuses circonstances, notamment pour déterminer dans quelle direction faire défiler une carte quand l'utilisateur clique dessus du bouton droit de la souris et déplace la souris tout en maintenant ce bouton appuyé.
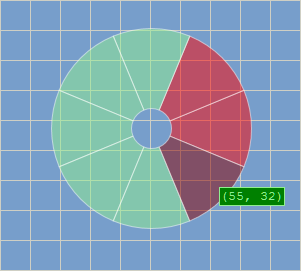
Dans ce cas, il faut déterminer laquelle des huit directions possibles emprunter (prévoir plus de directions est extrêmement déroutant pour l'utilisateur ! c'est une de ces occasions où il apprécie que la machine ne réagisse pas à la lettre à ses actions, mais seulement au-delà des limites d'une large tolérance...) Cela revient à déterminer lequel des huit secteurs de 45 degrés ayant pour sommet le point cliqué contient le point survolé par le pointeur (en rouge, sur ce pavé directionnel qui fournit un repère visuel à l'utilisteur tandis qu'il fait défiler la carte, les directions impraticables car le mouvement bute sur les limites de cette dernière) :
Les maths
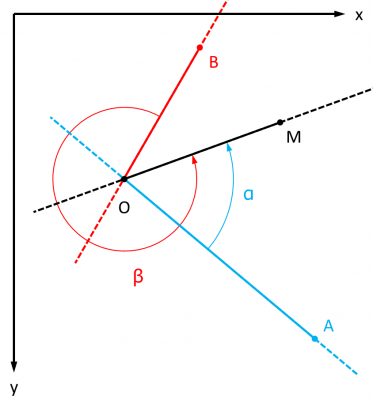
Nous avons déjà vu comment déterminer la position d'un point par rapport à une droite. C'est un calcul qui s'appuie sur le produit vectoriel pour déterminer si l'angle que le vecteur joignant deux points de la droite et le vecteur joignant un point de cette droite et le point dont la position est testée est plus grand que 180 degrés. En l'espèce il faut considérer deux angles α et β :
Il faut donc calculer deux produits vectoriels et de tester leurs signes pour déterminer si M est "au-dessus" de OA et "en dessous" de OB.
- cpAM = (yA - yO) * (xM - xO) - (xA - xO) * (yM - yO)
- cpBM = (yB - yO) * (xM - xO) - (xB - xO) * (yM - yO)
Le signe du produit vectoriel permet de définir une norme de position d'un point par rapport à une droite. En l'occurrence :
- Si le produit vectoriel est > 0, le point est "au-dessus" de la droite
- Si le produit vectoriel est < 0, le point est "en dessous" de la droite
De là, il suffit d'étudier la combinaison des signes des produits vectoriels pour déterminer le quadrant défini par les droites OA et OB sécantes en O dans lequel se trouve le point M (en rouge et en bleu) :
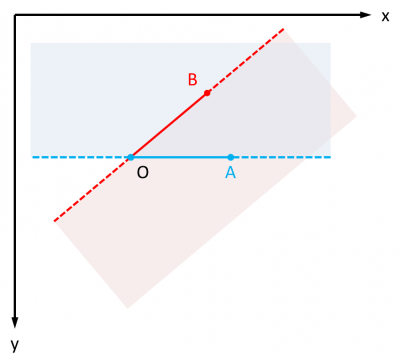
Toutefois, cette solution ne convient que si l'angle de sommet O et allant de A à B est inférieur ou égal à 180 degrés. En effet, si l'angle est supérieur à 180 degrés, alors le seul quadrant qu'il est possible d'isoler en étudiant la combinaison des signes des produits vectoriels correspond à la région où M n'est pas dans le secteur (en blanc) :
C'est pourquoi il faut tester si l'angle est inférieur ou supérieur à 180 degrés avant de procéder à l'étude de la combinaison des signes des produits vectoriels. Ce qui revient à tester la position de B par rapport à OA en utilisant... encore un produit vectoriel.