Avant de me lancer éventuellement dans une nouvelle session de challenges sur Root Me, j'ai opté pour une approche moins humiliante du développement en reprenant quelques projets restés en rade. Entre autres, un projet de jeu d'aventure en vectoriel dans une page Web, à base de JavaScript et de WebGL.
A cette occasion, un petit malin m'a soufflé l'idée qu'il serait amusant de pouvoir passer d'une représentation en vectoriel, donc en 2D, à une représentation en 3D, plus spécifiquement en vue isométrique, sur le modèle de l'impressionnant Voxatron. S'il n'était pas question de prétendre produire une telle merveille, du moins était-il effectivement intéressant de s'y essayer.
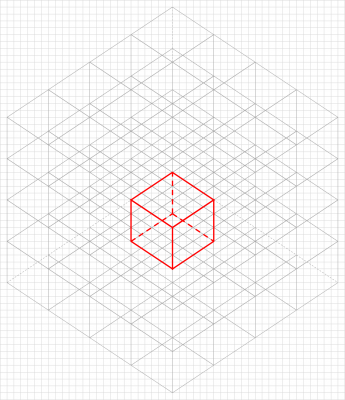
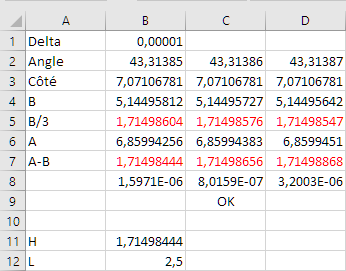
Comment donc produire un monde à base de voxels à l'aide de JavaScript et de WebGL, quelque chose qui ressemble grosso modo à cela ? :
Explication du service minimum à assurer pour y parvenir, en mobilisant toutefois du code déjà longuement présenté dans différents articles sur ce blog.
Avertissements
Cet article commentant le code plutôt que proposant de le réécrire, il est indispensable que vous consultiez ce code en parallèle. Cliquez ici pour tester le monde en voxels, et là pour récupérer une archive contenant tout le code correspondant.
Par ailleurs, vous êtes invité à tenir compte des points suivants :
- Je vais présumer que vous savez programmer en JavaScript, ce qui implique notamment que vous en maîtrisiez la véritable nature : un langage orienté objet à base de prototypes, et non à base de classes. Je n'utilise pas les classes, cette perversion intellectuelle honteusement intégrée au standard ECMAScript pour "faciliter" la vie des médiocres - ce n'est d'ailleurs que du sucre syntaxique.
- Même si je rappellerai quelques notions de 3D au passage, je vais aussi présumer que vous savez déjà commander le rendu d'un objet en 3D avec WebGL. Autrement, vous pouvez notamment vous reporter à divers articles sur ce blog, notamment dans cet article et sa suite pour ce qui concerne la prise en main des shaders.
- Si vous fréquentez un peu ce blog, vous devez désormais vous douter que dans la mesure du possible, je n'utilise jamais de code tiers : pas de bibliothèques, pas de composants, pas de frameworks, etc. En l'espèce, de la manipulation des matrices à la gestion des événements, tout dans ce projet est fait maison, attaquant directement les API exposées par le navigateur.
Quelques bibliothèques de base
Ce n'est pas parce que je n'utilise pas de bibliothèques tierces que je n'ai pas réalisé les miennes. Si j'ai évité d'y faire référence dans le code jusqu'alors produit sur ce blog, qui à en extraire du code pour le reprendre dans des exemples, c'était pour simplifier la compréhension des projets présentés. Toutefois, ce projet est assez conséquent pour qu'il ne soit plus raisonnable de tenir ce raisonnement. Il comprend donc sur les bibliothèques suivantes :
| libTOOLS.js | Quelques fonctions pratiques, telles que libTOOLS.randomInt () pour générer un entier aléatoire compris entre deux bornes, ou encore libTOOLS.createEventListener () pour créer un gestionnaire d'événements pouvant référencer un objet via this et recevoir des valeurs en paramètres sur le modèle de ce qui a été expliqué dans cet article. |
| libCANVAS.js | Une simple méthode libCANVAS.createCanvasWGL () pour créer le canvas dans lequel la scène est affiché par WebGL. |
| libWEBGL.js | Des objects libWEBGL.Vector3D et libWEBGL.Matrix3D pour manipuler des vecteurs 4x1 et des matrices 4x4 qui permettent de les transformer, ainsi que des objet libWEBGL.FragmentShaderHelper et libWEBGL.VertexShaderHelper pour faciliter la création de vertex shaders et de pixel shaders, sur le modèle de ce qui a été expliqué dans cet article. |
Par souci de ne pas compliquer la lecture du code, j'ai allegé le code de ces bibliothèques, qui ne comprend donc que ce qui est requis pour le présent projet. Une exception qui confirme la règle : libWEBGL.js, qui contient tout ce qu'elle contient actuellement, notamment des objets représentant des vecteurs 3x1 et des matrices 3x3 pour les transformer, l'usage de ces objets étant réservé à des projets qui s'appuient sur WebGL pour du rendu vectoriel, donc en 2D.
Ces bibliothèques ne sont pas basées sur un système de factorisation du code sous forme de module comme CommonJS ou plus récemment ECMAScript 6, la modularisation faisant depuis cette édition du standard partie intégrante de JavaScript. En effet, j'avais cherché une solution pour factoriser avant ES6, et sans sentir la nécessité de m'appuyer sur CommonJS, car YAGNI. Fidèle à mes habitudes, je suis donc resté simple.
Par exemple, libWEBGL se présente simplement sous la forme d'un objet
libWEBGL dont la déclaration est importée dans le programme qui l'utilise. Cet objet contient des méthodes, destinées à être appelées directement pour réaliser une tâche ou pour créer un objet - des fabriques, une concession pour ne pas trop insulter l'avenir. En l'espèce, l'objet libWEBGL ne contient que des fabriques :
var libWEBGL = {
createVSHelper: function (gl) {
return (new this.VertexShaderHelper (gl));
},
createFSHelper: function (gl) {
return (new this.FragmentShaderHelper (gl));
},
createMatrix2D: function (m) {
return (new this.Matrix2D (m));
},
createVector2D: function (v) {
return (new this.Vector2D (v));
},
createMatrix3D: function (m) {
return (new this.Matrix3D (m));
},
createVector3D: function (v) {
return (new this.Vector3D (v));
}
};
Plus loin dans le code de libWEBGL, on trouve la déclaration des constructeurs des objets appelés par les fabriques, et tout ce que ces objets contiennent. Par exemple, pour
Vector3D :
// Le constructeur
libWEBGL.Vector3D = function (v) {
this.v = new Array (4);
if (v === undefined)
this.origin ();
else
this.load (v);
};
// Une méthode .load ()
libWEBGL.Vector3D.prototype.load = function (v) {
var i;
for (i = 0; i !== 4; i ++)
this.v[i] = v[i];
return (this);
};
// Une propriété .x pour le coup définie avec des accesseurs
Object.defineProperty (libWEBGL.Vector3D.prototype, "x", {
get: function () { return (this.v[0]); },
set: function (x) { this.v[0] = x; }
});
// Etc.
Quant à la manière d'inclure la déclaration de l'objet
libWEBGL dans un programme, c'est par une simple inclusion de script via la balise idoine :
<script type="text/javascript" src="libWEBGL.js"></script>
Une vue "isométrique"
D'un point de vue graphique, les jeux en vue isométrique sont indéniablement ceux que je préfère. Des productions telles que Cadaver ou Viewpoint sont des petits chef-d'oeuvre où les maîtres du pixel art expriment véritablement tout leur talent. Par conséquent, pour ce monde en voxels, j'ai décidé d'opter pour ce type de représentation.
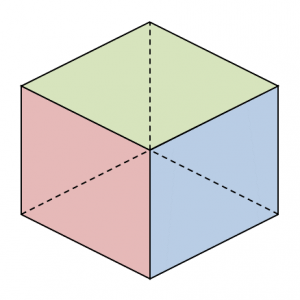
Enfin, pas tout à fait. C'est de l'isométrique, mais pas au sens strict. En effet, l'isométrique est un type de projection orthogonale, alors que nous allons utiliser une projection en perspective, parce qu'elle ne coûte pas plus cher et qu'elle rajoute beaucoup au rendu. Ce que nous allons retenir de l'isométrique, c'est l'idée de limiter l'amplitude de l'angle sous lesquel le joueur contemple la scène, de telle sorte que seules les faces du dessus, droite et avant d'un voxel soient éventuellement visibles, les autres étant toujours cachées - ce qui permettra d'ailleurs une belle économie de primitives.
De nos jours, ce qui est désigné par le terme de "voxel" n'a plus qu'un très lointain rapport avec la géniale astuce popularisée dans un jeu tel que Commanche. Dans un jeu tel que Minecraft et tout ce qui s'en inspire, un voxel désigne simplement un cube.
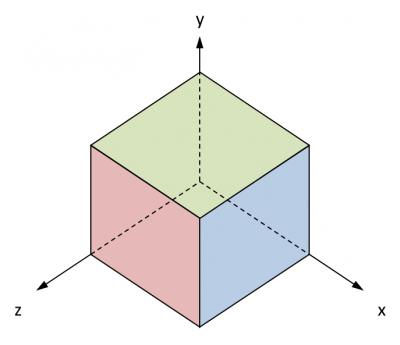
Dans notre projet, un voxel sera donc un petit cube aligné sur les axes du repère, qu'on rappelle être indirect dans WebGL, l'axe des affixes Z pointant vers le joueur :
Comme WebGL ne gère pas les quads, les faces de ce voxel seront composées à partir de triangles, décrits à l'aide de coordonnées de points et d'indices. Les indices seront donnés dans l'ordre qui permet de parcourir des points dans le sens des aiguilles d'une montre, le point de départ important peu. Par exemple, la face avant :
En effet, dans WebGL, l'élimination des faces cachées frappe celles dont l'ordre de parcours des projections des points s'effectue dans le sens contraire des aiguilles d'une montre, ou pour le dire autrement : le culling est CCW ("counter clockwise") par défaut.
L'isométrique optimisé, c'est 43,31386... degrés
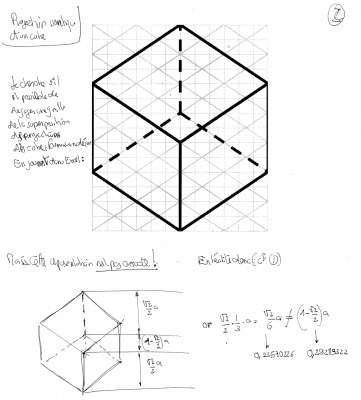
Ce qui suit n'est pas inutile à lire, mais le petit malin qui m'a suggéré de travailler un monde en voxels me fait remarquer que la vue isométrique adoptée dans un jeu tel que Cadaver adopte un angle encore plus faible, l'angle avant de la face du dessus coincidant avec l'angle arrière de la face du dessous dans la projection d'un voxel :
A vous de voir ce qui vous convient le plus. Quoi qu'il en soit, si vous souhaitez calculer l'angle correspondant, vous pouvez toujours vous référer aux calculs qui suivent.
S'il devait s'agir d'une représentation strictement isométrique, autant tricher un peu pour se simplifier la vie, tout particulièrement pour ce qui concerne le ray picking - identifier le voxel qui se trouve sous le pointeur de la souris.
En effet, dans une représentation strictement isométrique, le joueur observe la scène après qu'elle a subi une rotation de 45 degrés autour de l'axe des abscisses puis une rotation de -45 degrés autour de l'axe des ordonnées, histoire que son axe des affixes pointe vers la gauche tandis que son axe des abscisses pointe vers la droite, comme sur la figure représentant le voxel plus tôt.
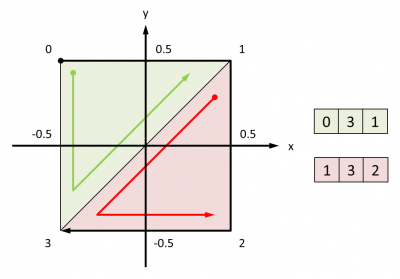
Ce qui serait pratique, c'est que la projection de la scène soit composée d'un motif périodique, de type losange. En effet, il serait alors assez simple de faire le lien entre tout ce qui survient dans la surface de projection et ce qui survient dans l'espace, et inversement. Typiquement, concevoir une sorte de z-buffer à la granularité du motif, qui permettrait de récupérer immédiatement l'identifiant du voxel dont une partie est rendu dans le motif qui contient un certain pixel, ce qui constituerait une simplification radicale du ray picking.
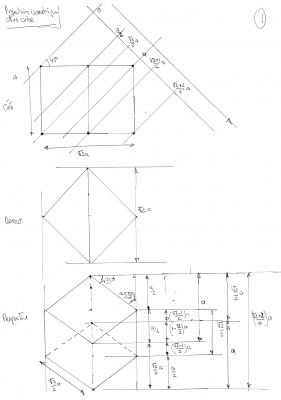
En travaillant sur une maquette dans un éditeur vectoriel permettant de caler le dessin sur un quadrillage bien régulier, il semble que la chose soit possible. Le motif est révélé totalement à partir de la constitution de la projection d'un bloc de 4x4 voxels :
En fait, ce travail fait implicitement l'économie d'une réflexion sur les angles sous lesquels le joueur contemple la scène. En effet, si ces angles sont tels que mentionnés plus tôt, les calculs sur la représentation théorique permettent d'établir les dimensions suivantes :
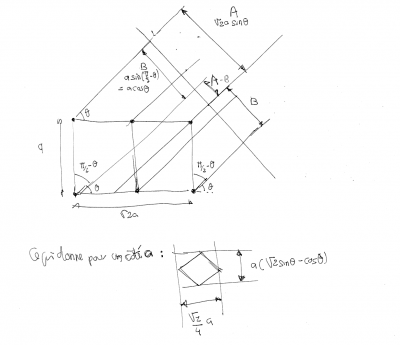
Les calculs des dimensions de ce losange en fonction de l'angle de rotation de la scène autour de l'axe des abscisses débouchent sur ces résultats :
- largeur de
- hauteur de
La recherche empirique de l'angle pour que la projection de la scène corresponde à la maquette permet de révéler que l'angle devrait être de l'ordre de 43,31386... degrés. Peu importe le côté, ici il a été fixé à 10 :
Une architecture des plus basiques
L'architecture du code est particulièrement dépouillée. Au chargement de la page, l'événement
onload entraîne l'appel à la fonction run () qui procède à quelques initialisations, soit essentiellement la création du canvas et la création d'un objet Demo, où tout le code de la démonstration est factorisé plutôt que d'encombrer l'objet window.
S'agissant d'un bête gestionnaire central, l'objet
Demo peut être détaillé tout de suite :
Demo () |
Constructeur, qui crée les objets Renderer et Scene, et pose les bases de la gestion de l'animation et des événements - la pression des touches de direction pour permettre au joueur de déplacer se deplacer dans le terrain. |
.destroy () |
A appeler par l'application qui crée l'objet Demo quand elle le détruit. |
.refresh3D () |
Rafraîchit l'affichage de la scène. Se contente d'appeler Scene.refresh (), mais pourrait par exemple aussi agir en fonction du résultat d'opérations réalisées lors de ce rendu, comme gérer les collisions. |
.refresh () |
Commande toutes les opérations à effectuer chaque fois qu'il faut rafraîchir l'affichage à l'échelle de l'objet Demo. Se contente d'appeler Demo.refresh3D (), mais pourrait aussi mettre à jour d'autres éléments de l'interface, comme une minimap. |
.start () |
Démarre l'animation via window.requestAnimationFrame (), en l'espèce l'oscillation de la scène autour de l'axe des ordonnées dans l'amplitude permise par la représentation "isométrique". |
.step () |
Appelée à chaque étape de l'animation par window.requestAnimationFrame (). Vérifie que le délai entre deux images s'est bien écoulé. Si c'est le cas, appelle Demo.animate (), qui appelle Scene.animate (), qui appelle SceneObject.animate ()de chaque objet 3D. Pour finir, appelle évidemment Demo.refresh (). |
.stop () |
Arrête l'animation en cours et la réinitialiser en vue d'un prochain redémarrage, en particulier en appelant Scene.resetAnimation (). Même logique que pour Demo.animate () : en cascade, finit par provoquer l'appel de SceneObject.resetAnimation () de chaque objet 3D. |
.onSceneKeyDown () |
Gestionnaire d'événement correspondant à la pression d'une touche. Plus spécifiquement, permet à le joueur de se déplacer dans le plan XZ dans les quatre directions et dans les limites du terrain, en pressant les touches de direction correspondantes. Pour cela, se contente d'appeler Scene.moveViewTo (). Puis, évite que la pression de la touche ne soit traitée à plus haut niveau, tout particulièrement au niveau de l'objet window, en appelant sa méthode .preventDefault (). Enfin, appelle évidemment Demo.refresh (). |
Au-delà de l'objet
Demo, les deux principaux objets sont Renderer et Scene. Par souci de clarté, une distinction est faite entre ce qui concerne le rendu, factorisé dans Renderer, et ce qui concerne la gestion de la scène, factorisé dans Scene. Les autres objets concernent la scène. Cette dernière est composée d'objets 3D représentés par des objets qui dérivent de l'objet SceneObject. Ici, il n'y a qu'un objet 3D : le terrain, représenté par l'objet Landscape. Le terrain est composé de voxels. Un voxel est représenté par un objet Voxel, qui dérive lui aussi de SceneObject, mais qui n'a pas vocation à être géré comme un objet 3D, s'agissant d'un atome de ces derniers, à moins qu'il ne se soit sorti du terrain pour être traité comme une particule.
Ces objets vont maintenant être détaillés, à commencer par
Renderer.
Un rendu à base de liste
Comme expliqué, tout ce qui concerne le rendu est factorisé dans
Renderer. A sa création, et pour l'essentiel, cet objet :
-
initialise les matrices du pipeline de transformation qu'il contrôle, soit
Renderer.matrixW,Renderer.matrixVetRenderer.matrixP; - crée des helpers pour créer et gérer les shaders, sur le principe expliqué dans cet article.
- crée des objets de WebGL sur lesquels il n'est pas question de revenir par la suite : un buffer pour les points, un autre pour les indices, et enfin un VAO.
Un mot sur les matrices. Très classiquement, le rendu d'une scène débute par la transformation des objets 3D qui la composent. Il s'agit d'appliquer à ces derniers successivement :
-
une transformation locale, via la matrice propre à l'objet
SceneObject.matrix; -
une transformation commune, via la matrice de la scène
Renderer.matrixW; -
une tranformation qui rapporte dans le repère du joueur - autrement dit, de la vue -, via la matrice de la vue
Renderer.matrixV; -
une projection telle que décrite longuement dans cet article, via la matrice de projection
Renderer.matrixP.
Pourquoi ne pas avoir positionné les trois dernières matrices dans
Scene ? Parce que Renderer doit fournir ces matrices à WebGL, ce qui implique qu'il doit pouvoir y accéder, et aussi parcequ'il doit rester agnostique quant aux objets dont il commande le rendu à WebGL, ce qui implique qu'il ne doit pas avoir à farfouiller dans Scene pour cela. A la limite, elles auraient pu être casées dans un objet Observer...
Au-delà, l'objet
Renderer fonctionne sur le principe d'une liste d'objets à rendre qui partagent assez de caractéristiques pour qu'il soit possible d'en commander le rendu à WebGL via un seul appel à drawElements (). Pourquoi ? Parce que comme expliqué ici, appeler une fois drawElements () pour un ensemble d'objets permet de les rendre bien plus rapidement qu'en appelant une fois cette méthode par objet.
Pour rappel, cela ne va pas sans faire des concessions. En l'espèce, les objets 3D doivent utiliser le même format de point et le même type de primitive, et aussi subir les mêmes transformations. Toutefois, il est possible d'intégrer la transformation d'un objet 3D au format de point sous la forme d'un attribut supplémentaire de type
mat4, auquel cas cette dernière contrainte est levée. L'inconvénient, c'est que cela entraîne une plus grosse consommation de l'espace mémoire et de la bande passante car il y a plus de données à transférer au GPU - des données par ailleurs redondantes, car la matrice locale est la même pour tous les points de l'objet 3D. Toutefois, le nombre de points est ici ridicule en comparaison des capacités du matériel, si bien que cette solution est retenue.
Le format de point commun à tous les objets 3D est donc le suivant :
x, y et z |
Un vec3 pour les coordonnées du point |
mL |
Une mat4 pour la matrice de transformation de l'objet 3D |
r, g et b |
Un vec3 pour la couleur du point |
Sachant que tous les objets 3D utilisent le même format de point et le même type de primitive, le fonctionnement est assez simple.
Scene.refresh () appelle successivement :
-
Renderer.renderStart ()pour indiquer qu'il va lui fournir les points et les indices des objets 3D qui subissent la même transformation ; -
Renderer.setMatrixW ()pour fournir la matrice de transformation commune des objets 3D ; -
Renderer.render ()pour fournir les points et les indices d'un objet 3D, et cela pour chacun des objets à rendre ; -
Renderer.renderEnd ()pour indiquer qu'il a fourni tous les éléments évoqués.
Dans le cas présent,
Renderer.render () se contente de rajouter l'objet 3D dans une liste qui est passée en revue par Renderer.renderEnd () pour charger les points et les indices avant d'appeler drawElements (). Toutefois, l'idée derrière cette liste, c'est qu'elle pourrait un jour contenir des objets 3D hétéroclites - pas le même format de point et/ou pas les mêmes transformations, ces dernières n'étant pas intégrées au format de point -, et que Renderer.renderEnd () se livrerait alors à toute une analyse pour en optimiser le rendu par groupe d'objets 3D partageant les mêmes caractéristiques.
Il n'y a pas plus à dire sur
Renderer, sinon peut-être que certains pourraient se demander pourquoi les matrices sont manipulées via des méthodes Renderer.setMatrix... () et Renderer.getMatrix... () et non des propriétés dotées d'accesseurs get et set. La seule raison, c'est qu'il était pratique de pouvoir appeler Renderer.setMatrix... () sans paramètre pour réinitialiser la matrice correspondante à sa valeur par défaut.
Un terrain à base de voxels
Ainsi,
Scene.objects ne contient qu'un objet 3D, à savoir un objet Landscape qui dérive de l'objet SceneObject. En tant que tel, Landscape comprend quelques propriétés et méthodes propres à tout objet 3D :
.isVisible |
Drapeau à true si l'objet doit être rendu. |
.setVisibility () |
Modifie la visibilité de l'objet depuis l'extérieur de ce dernier - un accesseur sur .isVisible aurait tout autant fait l'affaire. |
.matrix |
Matrice de transformation locale - ie : dans son repère - de l'objet. |
.animate () |
Progresse d'une étape dans l'animation de l'objet, par exemple en incrémentant l'angle d'une rotation. |
.resetAnimation () |
Réinitialise l'animation de l'objet, par exemple en restaurant la valeur par défaut de l'angle de la rotation. |
.load () |
Récupère les points et les indices nécesaires pour le rendu de l'objet, et quelques informations afférentes comme le nombre de primitives et le nouvel offset à rajouter aux indices par la même méthode d'un autre objet, qui serait appelée après. |
Vient ensuite l'objet
Landscape. C'est un objet composé de voxels, si bien qu'il n'est guère suprenant d'y trouver un tableau à trois dimensions Landscape.voxels, qui contient des objets Voxel. Ce tableau est peuplé lors de la construction de l'objet Landscape, en deux temps :
-
tout d'abord, par un appel à
Landscape.buildHeightmap (); -
dans la foulée, par un appel à
Landscape.buildMesh ().
Pourquoi deux méthodes et pas une ? Par simple souci de clarification, car nous sommes sur deux sujets différents, selon qu'il s'agit de créer un tableau
Landscape.heightmap des hauteurs des colonnes de voxels - mesurées en voxels -, et selon qu'il s'agit d'utiliser ce tableau pour générer un maillage, en l'occurrence le tableau Landscape.voxels. Surtout, si nous devions pousser plus loin les feux, il pourrait devenir nécessaire d'envisager un chargement par chunk du terrain. Dans ces conditions, la génération de la table des hauteurs pourrait sans doute toujours s'effectuer une fois pour toute, mais la génération de son maillage devrait être progressive, sous peine de saturer la mémoire.
Landscape.buildHeightmap génère donc un tableau Landscape.heightmap à l'aide d'un algorithme de génération de terrain quelconque. Pour l'occasion, un algorithme de génération de labyrinthe présenté dans cet article a été recyclé en un clin d'oeil, d'où la présence de méthodes Landscape.carveTunnels () et Landscape.carveRooms ().
Générés à partir de ce tableau des hauteurs par
Landscape.buildMesh (), le maillage se présente comme un sol avec des murs composés de colonnes de trois voxels de hauteur.
Après l'occasion de sa création, les couleurs par défaut
LANDSCAPE_COLORS des faces d'un voxel sont modulées en fonction de sa hauteur par application d'une bête formule d'interpolation linéaire entre la hauteur minimale Landscape.heightMin et la hauteur maximale Landscape.heightMax trouvées dans le tableau des hauteurs :
const LANDSCAPE_COLORS = [ // Devant 0.5, 0.0, 0.0, // Gauche 0.5, 0.5, 0.0, // Dessus 0.0, 0.5, 0.0, // Arrière 0.0, 0.5, 0.5, // Droite 0.0, 0.0, 0.5, // Dessous 0.5, 0.0, 0.5 ]; colors = new Array (); for (i = 0; i != LANDSCAPE_COLORS.length; i ++) colors.push (LANDSCAPE_COLORS[i] * (0.5 + (y - this.heightMin) / (this.heightMax - this.heightMin))); voxel = new Voxel (VOXEL_SIDE, colors=colors);
Le point le plus important, c'est que certaines faces d'un voxel n'ont jamais vocation à être affichées dans la vue "isométrique" : les faces de dessous, gauche et arrière. Pour cette raison, l'initialisation d'un voxel se poursuit en rendant systématiquement ces faces invisibles :
voxel.visibleFaces[voxel.FACE_BOTTOM] = false; voxel.visibleFaces[voxel.FACE_LEFT] = false; voxel.visibleFaces[voxel.FACE_BACK] = false;
D'autres faces n'ont elles aussi pas vocation à être affichées : les faces visibles d'un voxel par lesquelles il est relié à d'autres voxels, dites faces mitoyennes. Ces faces sont donc aussi rendues invisibles :
if ((y >= 1) && this.voxels[y - 1][z][x]) this.voxels[y - 1][z][x].visibleFaces[voxel.FACE_TOP] = false; if ((z >= 1) && this.voxels[y][z - 1][x]) this.voxels[y][z - 1][x].visibleFaces[voxel.FACE_FRONT] = false; if ((x >= 1) && this.voxels[y][z][x - 1]) this.voxels[y][z][x - 1].visibleFaces[voxel.FACE_RIGHT] = false;
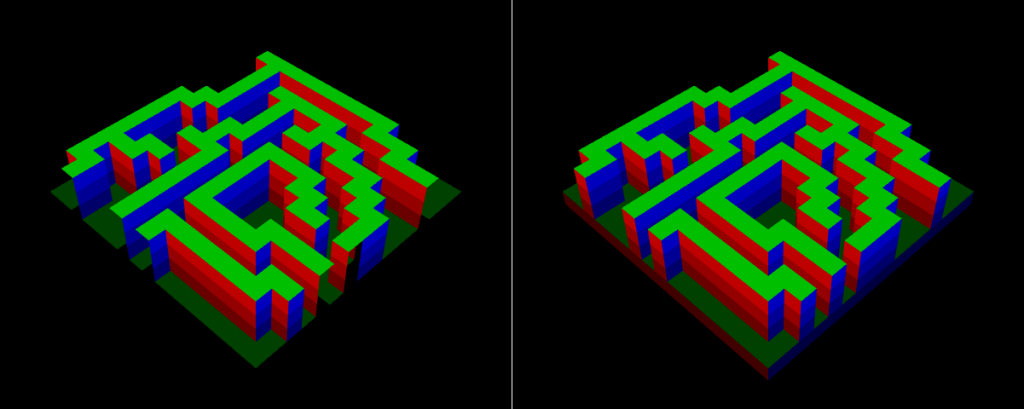
Toutefois, cette invisibilité ne peut être que temporaire. En effet, une face mitoyenne doit être rendue visible si jamais le voxel voisin disparaît, soit qu'il est détruit, soit qu'il n'est pas affiché parce qu'il se trouve en dehors de la partie du terrain représentée - la vue. La figure suivante illustre ce dernier cas :
Ici, seul ce cas est géré. Chaque fois que la position de la vue dans le terrain est modifié par appel à
Landscape.moveViewTo () via Scene.moveViewTo (), les voxels qui se trouvent sur les faces avant et droite du volume englobant cette vue à sa précédente position sont passés en revue pour rendre invisibles la face avant des premiers et la face droite des seconds, et le même passage en revue est repété une fois la vue déplacée pour rendre visibles les faces concernées des nouveaux voxels concernés.
Pour achever ce tour de
Landscape, il convient d'expliquer comment Renderer récupère ses points et ses indices pour alimenter drawElements (). Cela passe par un appel à Landscape.load (), qui appelle Voxel.load () pour chaque voxel rencontré dans Landscape.voxels. A son tour, Voxel.load () calcule la matrice de transformation si le voxel est animé - autrement, ce sera une matrice identité -, puis crée les points selon le format de point présenté plus tôt, en s'en tenant aux points qui composent les faces indiquées comme visibles dans Voxel.visibleFaces.
Les voxels, atomes des objets 3D
Ce qui conduit à parler de l'objet
Voxel. Ses propriétés décrivent un cube, comme expliqué plus tôt :
.vertices |
Tableau des coordonnées (x, y, z) des quatre points de chaque face. |
.colors |
Tableau des couleurs (r, g, b) de chaque face. |
.indices |
Séquence des indices des points composant les deux triangles de chaque face. |
.visibleFaces |
Tableau des drapeaux indiquant si une face est visible ou non. |
Par défaut un cube de 1.0 de côté centré sur l'origine du repère de la scène, un voxel doit au minimum subir une translation pour être placé là où il faut dans le terrain. Pour cela,
Scene.buildMesh () appelle Voxel.translate () qui procède à une translation irréversible des 16 points, sommets des 6 faces du voxel.
Optimiser un voxel, c'est possible, mais dans quelles limites ?
Décrire un voxel à l'aide de 4 points par face, soit 16 points, au lieu de simplement 8 points entre les faces, vraiment ?
Hélas, dans le système de rendu que nous avons adopté pour rendre tous les voxels en un seul appel à
drawElements (), le fragment shader doit tirer la couleur d'une face de la couleur de ses points, et non d'une uniforme. Par conséquent, il faut que chaque face dispose de ses propres points qui codent sa couleur. La critique n'est donc pas recevable.
Une critique plus audible, c'est : pourquoi 16 points, au lieu de 12 points pour décrire seulement les faces visibles, puisque ce sont toujours les trois mêmes qu'un voxel expose ?
C'est juste, il y aurait ici matière à économies. Toutefois, cela impliquerait que le voxel soit statique, pour ne jamais avoir prendre le risque d'exposer une de ses faces qui n'existent pas. Dans ce cas, en plus d'offrir l'occasion d'économiser sur le nombre de points, cela offrirait celle d'économiser sur la mémoire, car dès lors qu'un voxel serait statique, sa position dans le terrain pourrait être inscrite dans ses coordonnées plutôt que résulter de l'application d'une translation via la matrice figurant dans le format de point.
Il resterait possible d'animer un voxel en y substituant un cube. Il faudrait alors affiner la manière dont
Renderer traite la liste des objets 3D à rendre, en lui permettant de distinguer des groupes d'objets : rendu des objets 3D composés de voxels subissant les mêmes transformations et basés sur le format de point (x, y, z, r, g, b), et rendu des autres objets 3D subissant des transformations spécifiques et basés sur le format de point (x, y, z, r, g, b, mL), chaque rendu étant réalisé par un appel à drawElements (). Vous comprenez maintenant pourquoi cette liste...
Plus généralement, partant d'un terrain composé de cubes, la volonté d'optimiser conduit à toujours plus chercher à faire du terrain un maillage composé des faces visibles des voxels, et donc à prendre toujours plus de distance avec la notion même de voxel. C'est donc au risque de s'égarer, car il faut se rappeler l'objectif : produire un monde à base de voxels, l'idée que chaque voxel pourra faire l'objet d'une gestion particulière, par exemple pour le supprimer au terme d'une animation quand le joueur creuse le terrain. A moins d'élaborer un algorithme sophistiqué qui construirait le maillage avant d'en commander le rendu - dont il n'est pas dit qu'il serait plus performant que le rendu d'un ensemble de voxels sous forme de cubes, voire même de trifaces -, il faut donc reconnaître aux voxels le droit d'exister au moment du rendu, et ne pas pousser trop loin en matière d'optimisation.
Dans le cadre de cet article, quand bien même elles seraient fort simples à mettre en oeuvre, les optimisations qui permettraient de dissocier un voxel d'un cube sont restées dans les cartons. Cela signifie qu'un voxel comprend tout ce qui est requis pour l'animer comme si c'était un cube, à ceci près qu'il est de plus possible de contrôler la visibilité de ses faces via
Voxel.visibleFaces pour tout de même éviter de charger la barque en évitant de commander le rendu des ses faces cachées. Cela ménage la possibilité d'animer la scène en gérant un voxel comme une particule après avoir rendu toutes ses faces visibles, comme par exemple pour l'éjecter lorsque le joueur clique dessus pour creuser le terrain :
.setTranslation () |
Définit une direction et une vitesse de translation le long des trois axes. |
.setRotation () |
Définit une rotation autour des axes des abscisses, des ordonnées et des affixes, successivement. |
.setScaling () |
Définit un facteur d'homothétie uniformément le long des trois axes. |
.resetAnimation () |
Restaure les valeurs initiales des transformations précédentes. |
.animate () |
Incrémente les variables permettant d'animer les transformations précédentes. |
Du ray picking pour une interaction de base
Tout ce qui vient d'être décrit est assez trivial, car grosso modo strictement technique. Ça l'est moins pour ce qui concerne le ray picking, opération qui consiste donc à identifier le voxel qui se trouve sous le pointeur de la souris.
Le ray picking s'appuie sur le ray casting, une technique déjà présentée dans cet article. Ici, il est possible d'exploiter des opportunités d'optimisation du fait de la représentation "isométrique" du terrain, tout particulièrement la périodicitié des voxels qui le composent, et leur alignement sur les axes du repère de la scène.
Un déplacement de la souris sur la scène provoque l'appel au gestionnaire d'événement
Demo.onSceneMouseMove (). Pour plus d'informations sur la manière dont une méthode peut être utilisée comme gestionnaire d'événement, ce qui implique de permettre l'accès à son objet via this et de lui passer des paramètres, reportez-vous à cet article.
Ce gestionnaire contient tout le code du ray picking, exception faite du calcul de l'intersection d'une droite et d'un plan, factorisé dans
Demo.planeIntersection (), car appelée en plusieurs occasions.
Comme dans le ray picking, tout commence par le calcul des coordonnées du point
rayEnd de la surface de projection - la face avant du volume de clipping - dont le pixel est la représentation dans le canvas. Cela implique une projection inverse, ce qui produit des coordonnées exprimées dans le repère de la vue :
r = this.wglContext.tag.getBoundingClientRect (); x = e.clientX - Math.round (r.left); y = e.clientY - Math.round (r.top); rayStart = libWEBGL.createVector3D (); rayEnd = libWEBGL.createVector3D ([ -NEAR * (x / (this.wglContext.width / 2.0) - 1.0), -NEAR * (1.0 - y / (this.wglContext.height / 2.0)), NEAR * 1.0, -NEAR ]); rayEnd.transform (this.scene.renderer.getMatrixP ().inverse ());
Issu de l'origine
rayStart du repère de la vue, le rayon passe par ce point. Disposant des coordonnées de l'un et de l'autre, il est possible de leur appliquer les transformations inverses par la matrice View puis la matrice World pour les exprimer dans le repère de la scène :
m = this.scene.renderer.getMatrixW (); m.multiply (this.scene.renderer.getMatrixV ()); m.inverse (); rayStart.transform (m); rayEnd.transform (m);
Les choses sérieuses commencent alors. Composition à base de voxels oblige, le volume englobant la partie du terrain représentée - la vue - est un parallélépipède aligné sur les axes du repère de la scène, autrement dit, une axis aligned bounding box, ou AABB. Trois objets sont créés, qui chacun représente un des plans dans lequel se trouve une face visible de cette AABB :
planeTop, planeRight, et planeFront pour les faces de dessus, droite, et avant, comme leurs noms l'indiquent.
Chaque plan est défini par un point et une normale dont les coordonnées sont exprimées dans le repère de la scène. Les coordonnées du point sont limitées à la coordonnée utile. Par exemple, pour
planeTop, c'est .yMin, puisque l'abscisse et l'affixe peuvent être considérées à 0. A cela s'ajoutent les bornes des coordonnées de la face correspondante. Pour continuer avec planeTop, la face du dessus s'étale dans le plan en abscisse entre .xMin et .xMax, et en affixe entre .zMin et .zMax.
Noter que les coordonnées de l'AABB retournées par
Scene.getViewBox () sont mesurées en voxels. Il faut en tenir compte pour les exprimer ici dans le repère de la scène. Ainsi, si view.x vaut 2 et que view.width vaut 3, cela implique que l'AABB s'étend en abscisse entre 2 * VOXEL_SIDE et (2 + 3) * VOXEL_SIDE, car l'AABB est définie par les faces extérieures des voxels.
In fine, cela donne :
view = this.scene.getViewBox ();
n = libWEBGL.createVector3D ([0.0, 1.0, 0.0, 1.0]);
planeTop = {
normal: n,
point: null,
yMin: view.y,
xMin: view.x,
xMax: view.x + view.width,
zMin: view.z,
zMax: view.z + view.depth
};
n = libWEBGL.createVector3D ([1.0, 0.0, 0.0, 1.0]);
planeRight = {
normal: n,
point: null,
xMin: view.x,
yMin: view.y,
yMax: view.y + view.height,
zMin: view.z,
zMax: view.z + view.depth
};
n = libWEBGL.createVector3D ([0.0, 0.0, 1.0, 1.0]);
planeFront = {
normal: n,
point: null,
zMin: view.z,
yMin: view.y,
yMax: view.y + view.height,
xMin: view.x,
xMax: view.x + view.width
};
Tout est maintenant en place pour dérouler l'algorithme. Ce dernier consiste à déterminer si le rayon rentre dans l'AABB, si oui par quel voxel, et à suivre alors le rayon de voxel en voxel jusqu'à atteindre un voxel du terrain ou alors sortir de l'AABB. Pour ce faire, c'est assez simple, en procédant en deux temps.
Dans un premier temps, il s'agit donc de déterminer si le rayon rentre dans l'AABB, et si oui par quel voxel :
- Calculer l'intersection du rayon avec les plans. Vue "isométrique" oblige, le rayon coupe nécessairement chacun des trois plans.
- Dans chaque cas, déterminer si le rayon se trouve dans les limites de la face dans le plan. Dans le cas où le rayon coupe deux, voire trois faces, retenir arbitrairement la première face trouvée. Si le rayon ne coupe aucune des faces, fin.
- Convertir les coordonnées de l'intersection en coordonnées de voxel, et vérifier dans la liste des voxels du terrain si ce voxel existe. Si oui, fin.
Dans un second temps, si le rayon rentre dans l'AABB mais par un voxel qui n'existe pas dans le terrain, il faut suivre le rayon :
-
Repositionner les plans au niveau des faces du voxel courant opposées à celles qu'ils contiennent. Par exemple,
planeTopest repositionné au niveau du plan parallèle qui contient la face de dessous du voxel courant - donc la face du dessus du voxel du dessous. - Reprendre les calculs d'intersection et de vérification de présence de l'intersection dans les limites des faces, en se contentant toujours de retenir la première face trouvée - elle existe forcément.
- Si le rayon sort de l'AABB, fin.
- Sinon, convertir les coordonnées de l'intersection en coordonnées de voxel, et vérifier dans la liste des voxels du terrain si ce voxel existe. Si oui, fin.
- Sinon, faire de ce voxel le voxel courant, et reboucler sur un repositionnement des plans.
Tout cela semble devoir nécessiter pas mal de calculs, mais c'est une illusion. En effet, comme déjà mentionné, la vue "isométrique" offre des opportunités d'optimisation. Deux sont principalement exploitées.
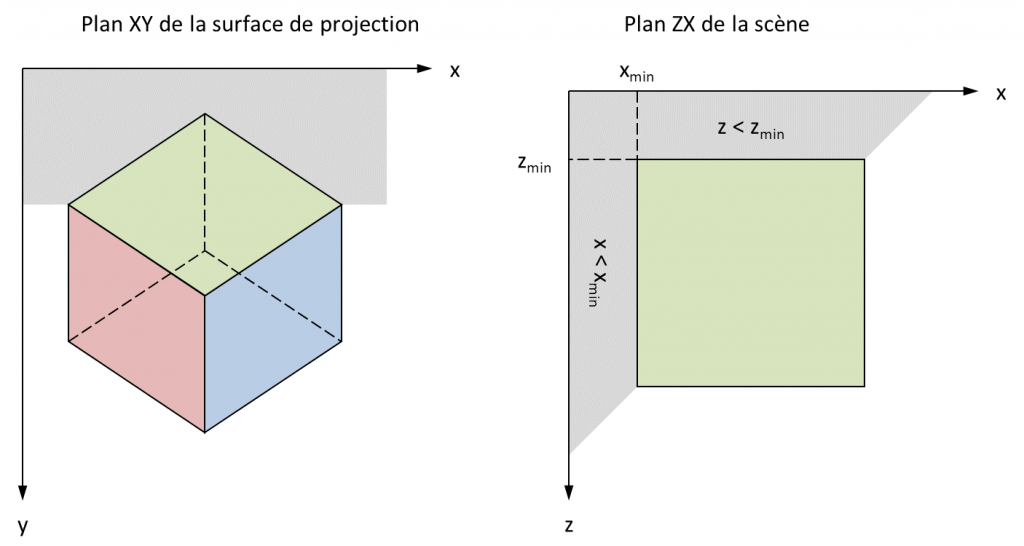
Une optimisation pour déterminer si le rayon coupe l'AABB. Très classiquement, le rayon passe à côté si jamais le pixel sous le pointeur de la souris se trouve en dehors du polygone englobant la projection de l'AABB à l'écran. Pour le déterminer dans le premier temps de l'algorithme, il faut simplement traduire en 3D le problème jusqu'alors exprimé en 2D. Cela revient à dire que le rayon passe à côté de l'AABB dans l'un ou l'autre de ces cas :
- il coupe le plan de la face du dessus à gauche ou derrière cette face dans ce plan ;
- il coupe le plan de la face avant à gauche ou sous cette face dans ce plan ;
- il coupe le plan de la face droite à droite ou derrière cette face dans ce plan.
Un dessin valant mieux qu'un long discours, en voici un pour bien comprendre :
Sur ces figures, si jamais l'intersection du rayon avec le plan de la face du dessus se trouve dans la zone grise, alors le rayon ne coupe pas l'AABB. Cela se comprend d'évidence en 2D, en contemplant la figure de gauche qui représente la projection du voxel : si le joueur pointe un pixel dans la zone grise, le rayon passe au-dessus de l'AABB. La traduction de cette évidence en 3D dans le repère de la scène montre que pour déterminer si l'intersection se trouve dans la zone grise, il suffit de comparer son abscisse et son affixe à des minima.
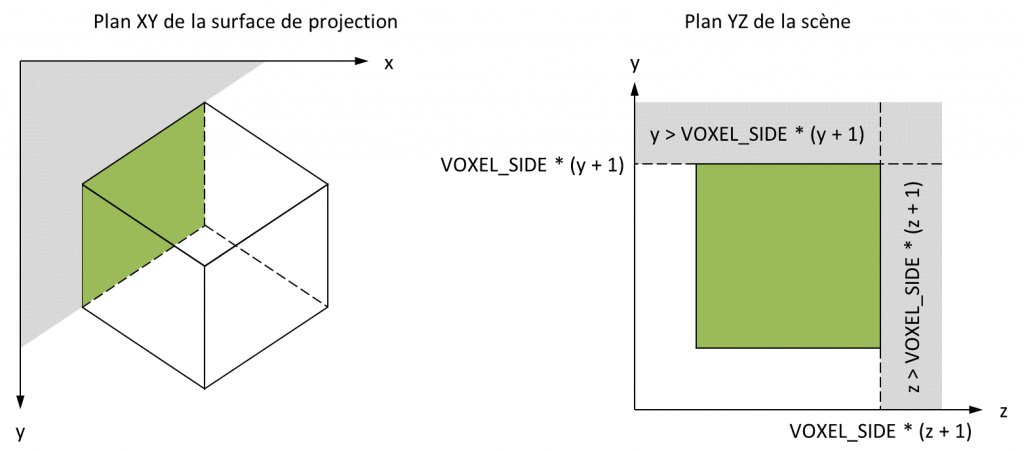
Une optimisation pour déterminer si une intersection avec un plan se trouve dans les limites de la face correspondante. Les voxels étant alignés sur les axes du repère de la scène, il suffit de procéder à des comparaisons pour cela. Par exemple, dans le second temps de l'algorithme, de telles comparaisons sont mises en oeuvre pour déterminer si le rayon sort d'un voxel en (x, y, z) en coupant sa face gauche, et s'il sort alors de l'AABB :
// Repositionner le plan de la face droite du voxel au niveau de la face gauche
planeRight.point = libWEBGL.createVector3D ([VOXEL_SIDE * x, 0.0, 0.0, 1.0]);
// Calculer l'intersection du rayon avec ce plan
point = this.planeIntersection (rayStart, rayEnd, planeRight.point, planeRight.normal);
// Vérifier si l'intersection est dans les limites de la face
//if ((point.y >= VOXEL_SIDE * y) &&
// (point.z >= VOXEL_SIDE * z)) {
if ((point.y >= (VOXEL_SIDE * y - EPSILON)) &&
(point.z >= (VOXEL_SIDE * z - EPSILON))) {
// Vérifier qu'il se trouve bien un voxel à gauche du voxel courant, car autrement le rayon est donc sorti de l'AABB
if (x === planeRight.xMin) {
done = true;
face = Voxel.prototype.FACE_LEFT;
}
else {
// Le voxel de gauche, dans lequel le rayon rentre donc par la face droite, devient le voxel courant
x--;
voxel = this.scene.landscape.voxels[y][z][x];
if (voxel)
done = true;
face = Voxel.prototype.FACE_RIGHT;
}
}
Comme il est possible de le constater, vérifier si l'intersection se trouve dans les limites de la face gauche se résume à vérifier si elle se trouve au-dessus de
(VOXEL_SIDE * y - EPSILON) et devant (VOXEL_SIDE * z - EPSILON). Pourquoi seulement deux comparaisons ? Car il suffit de tenir le même raisonnement que celui utilisé pour déterminer si le rayon coupe l'AABB. Si le rayon rentre dans le voxel, il ne peut en sortir que par une intersection qui appartient au voxel. En conséquence, cette intersection est déjà telle que son ordonnée est inférieure à (VOXEL_SIDE * (y + 1)), et son affixe déjà inférieure à (VOXEL_SIDE * (z + 1)) :
Kézako, le
EPSILON ? C'est une solution insatisfaisante à un problème qui n'en a pas de satisfaisante, et qui peut se formuler ainsi. Permettre au joueur de sélectionner une face en survolant un pixel de la représentation d'un voxel dans la surface de rendu, cela implique qu'un pixel ne peut jamais appartenir qu'à une seule face - les pixels des arêtes et des angles ne sont pas distingués des autres pixels des faces lors du rendu. Partant, le point de l'espace dont ce pixel est la représentation de la projection ne peut jamais appartenir qu'à une seule face dans l'espace. D'où la question : à quelle face justement, quand ce point se trouve sur une arête - intersection de deux faces - ou qu'il s'agit d'un angle - intersection de trois faces ? La réponse n'est pas évidente à donner, car par opposition à ce qui se passe dans le monde discret des pixels de la surface de rendu, les arêtes et les angles existent toujours dans le monde continu des points dans l'espace...
Pour répondre à cette question, il faut effectuer une première concession à la rigueur géométrique, en posant qu'un point d'une arête ou un angle ne peut appartenir qu'à une face. Cela implique d'utiliser une inégalité stricte d'un côté et pas de l'autre quand il s'agit de comparer une coordonnée à des bornes pour savoir si le point se trouve dans les limites d'une face :
xMin < x &ge xMax
Toutefois, cela ne suffit pas. Par exemple, voici les résultats retournés par
Demo.planeIntersection () dans le cas où le rayon coupe l'arête formée par l'intersection des plans des faces gauche et arrière du voxel (39, 4, 22) de côté VOXEL_SIDE = 0.1875 :
(7.3124999999999973, 0.8293580728609262, 4.1249999999999991, 1.0000000000000000)
Pour considérer que ce point se trouve dans les limites de la face gauche, il faudrait que notamment que
point.z >= VOXEL_SIDE * 22 = 4.125. Or ce n'est pas le cas, car l'affixe retournée est 4.1249999999999991, un nombre légèrement inférieur. Même problème avec la face arrière. Pour considérer que ce point se trouve dans les limites de cette face, il faudrait notamment que point.x >= VOXEL_SIDE * 39 = 7.3125, mais l'abscisse retournée est 7.3124999999999973, ici encore un nombre légèrement inférieur... Au total, aucune intersection avec une face cachée du voxel n'est trouvée, et tout part en sucette.
Comment résoudre ce problème ? Arrondir les coordonnées retournées par
Demo.planeIntersection () n'est certainement pas la solution. En effet, arrondir à combien de décimales ? Et est-on bien certain qu'il faudra arrondir à la décimale supérieure, comme il le faudrait ici, dans tous les cas ? Tout dépend de la précision des calculs au regard de l'échelle de grandeurs des valeurs utilisées, ce sur quoi bien malin serait celui qui pourrait statuer...
Quitte à toucher à des valeurs dans les inégalités, plutôt toucher à celles que l'on contrôle qu'à celles que l'on ne contrôle pas. La meilleure solution est de fixer une marge de tolérance
EPSILON en retrait des bornes, dont la valeur doit être déterminée empiriquement. Par exemple, la comparaison portera sur point.z >= VOXEL_SIDE * y - EPSILON = 4.125 - 0.001 = 4.124, et cette fois elle sera validée. Cela revient à dire que la face gauche est un peu plus grande qu'elle ne l'est réellement - elle démarre un peu plus bas qu'elle ne devrait. C'est une seconde concession à la rigueur géométrique.
Ces concessions laissent un goût amer, car tout cela peut n'apparaître pas très rigoureux. Toutefois, passer du monde continu des points dans l'espace au monde discret des pixels dans la surface de rendu entraîne nécessairement une perte d'information. Partant, il ne faut pas se faire d'illusion : à un moment ou à un autre, cela doit se payer par des approximations. Pour se consoler, on se dira que s'agissant de produire un jeu vidéo, seul le résultat compte...
In fine, si au terme de ce long processus un voxel qui existe dans le terrain est coupé par le rayon, la couleur de la face concernée est modifiée. Dans ce cas, comme dans celui où le voxel précédemment pointé ne l'est plus, un rendu est commandé via
Scene.refresh ().