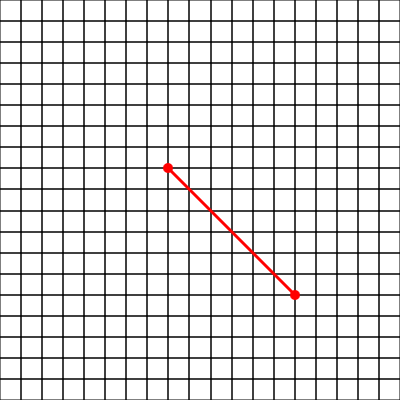
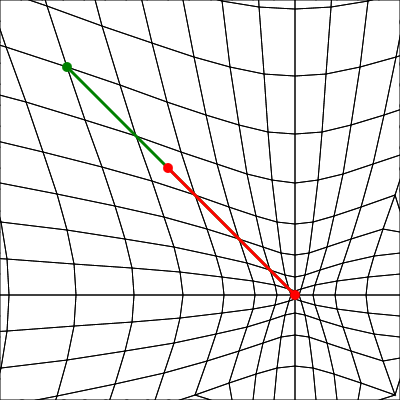
Comment déformer un maillage en modifiant la distance des points à un centre comme s'ils étaient attirés ou repoussés par ce centre selon une force dont l'intensité dépend de la distance ? Le résultat attendu est par exemple le suivant :
La solution
Un tel effet résulte très simplement de la translation de chaque point du maillage le long de l'axe qui le relie au centre, selon un facteur à moduler en fonction de la distance initiale entre le point et le centre.
Le code JavaScript
Le maillage est décrit dans un tableau de tableaux
meshBase[] où les points sont stockés sous la forme de structures {x, y} d'abord en ligne, puis en colonne. De la sorte, les coordonnées du point ligne 3 et colonne 7 sont mesh[3][7].x et mesh[3][7].y. Le tableau contient MESH_HEIGHT lignes et MESH_WIDTH colonnes de points. Il est généré de la manière suivante :
var MESH_WIDTH = 20, MESH_HEIGHT = 20;
var meshBase = new Array ();
for (j = 0; j != MESH_HEIGHT; j ++) {
meshBase.push (new Array ());
for (i = 0; i != MESH_WIDTH; i ++)
meshBase[j].push ({x:Math.round (i * r.width / (MESH_WIDTH - 1)), y:Math.round (j * r.height / (MESH_HEIGHT - 1))});
}
La déformation autour d'un point O est accomplie par une fonction qui calcule l'image de chaque point M du maillage par translation le long du vecteur OM d'un facteur
d / k. Dans ce facteur, d est la distance OM initiale et k est une constante, par exemple 100 (sa valeur est définie empiriquement, c'est-à-dire en fonction du résultat produit qui paraît le plus esthétique).
function meshDeform (xO, yO) {
var i, j, xM, yM, d;
for (j = 1; j != (MESH_HEIGHT - 1); j ++) {
for (i = 1; i != (MESH_WIDTH - 1); i ++) {
xM = meshBase[j][i].x;
yM = meshBase[j][i].y;
d = Math.sqrt ((xM - xO) * (xM - xO) + (yM - yO) * (yM - yO));
xM = (d / k) * (xM - xO) + xO;
yM = (d / k) * (yM - yO) + yO;
mesh[j][i] = {x:Math.round (xM), y:Math.round (yM)};
}
}
meshDraw ();
}
Les compteurs des boucles sont définis de telle manière que les points qui constituent les bordures du maillage ne subissent aucune translation. C'est une solution pour s'assurer que le résultat produit occupe quoi qu'il arrive toute la surface occupée par le maillage initial.
L'exemple
Cliquez ici pour accéder à une page de test minimaliste. Vous pourrez visualiser le code et le récupérer pour travailler avec.
Les maths
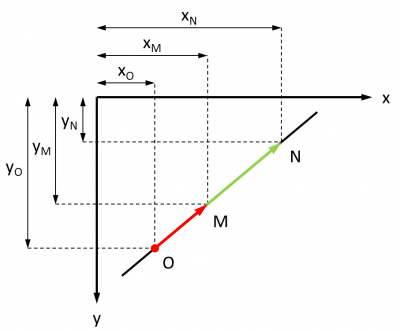
Chaque point M subit une translation le long du vecteur OM pour l'amener en N :
Quand la translation est d'un facteur k, alors ON = k * OM. Les coordonnées de N s'en déduisent :
xN - xO = k * (xM - xO)
donc :
xN = k * (xM - xO) + xO
De même pour yN :
yN = k * (yM - yO) + yO
Le calcul est effectué pour chacun des points du maillage (exception faite des points constituant les bordures, pour la raison déjà citée). Par exemple, le point (8, 8) repoussé par le point (14, 14) :
Ce qui donne :