Comment générer aléatoirement un nombre entier compris dans un intervalle, c'est-à-dire entre des valeurs minimale et maximale ? La solution qui vient spontanément à l'esprit (min + Math.round ((max -1) * Math.random ())) n'est pas correcte, car elle n'assure pas la représentativité statistique équitable (équiprobabilité) de tous les entiers possibles.

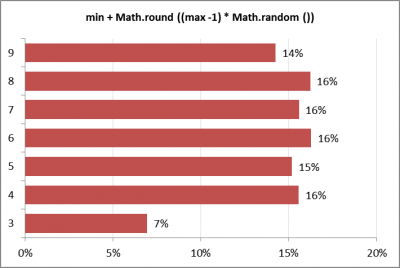
Par exemple, la répétition de 1 000 tirages d'une valeur dans l'intervalle [3, 9] permet de dégager les probabilités d'occurrence par valeur suivantes :

Pourquoi ce problème, et comment y remédier ?

Comme le graphique présenté permet de le constater, l'application de la solution qui vient spontanément à l'esprit conduit à une sous-représentation statistique de la valeur 3 ; plus généralement, la probabilité de la valeur minimale de l'intervalle est minorée.

La raison est que le code s'appuie sur Math.round (), qui va arrondir à 0 une valeur dans [0, 0.5[, à 1 une valeur dans [0.5, 1.5[, à 2 une valeur dans [1.5, 2.5[ etc. Le premier de ces intervalles à une amplitude de presque 0.5, tandis que les intervalles suivants ont une amplitude de presque 1.0. Bref, quand une valeur aléatoire (max -1) * Math.random () est générée, elle a deux fois moins de chances d'être arrondie à 0 que d'être arrondie à tout entier au-delà.

Il faut donc s'assurer que Math.round () sera appelée à arrondir des valeurs d'un intervalle d'amplitude de (presque) 1.0.

En JavaScript, la solution se traduit par le code suivant :

function randomInt (min, max) {
	return (min + Math.floor ((max - min + 1) * Math.random ()));
}

Cliquez ici pour accéder à une page de test minimaliste. Vous pourrez visualiser le code et le récupérer pour travailler avec.

Il s'agit d'éviter d'utiliser Math.round () pour arrondir une valeur dans [0.0, 0.5[ à 0. A la place, il faut utiliser Math.floor () pour arrondir une valeur dans [0.0, 1.0[ à 0.

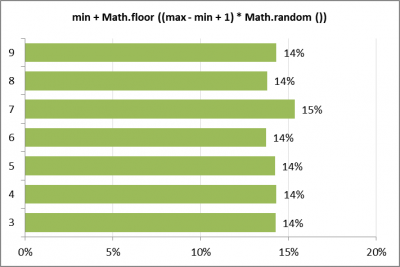
Pour reprendre l'exemple initial, la répétition de 1 000 tirages d'une valeur dans l'intervalle [3, 9] à l'aide de la solution permet de dégager les probabilités d'occurrence par valeur suivantes :

On constate l'équiprobabilité des valeurs entières dans l'intervalle [3, 9].