Comme il en a été question dans un long article sur le coding-of de Scoopex "TWO", Scoopex "ONE" était restée dans les cartons. En effet, au moment de la diffusion de Scoopex "TWO" sur Amiga 500, il s'était avéré que cette cracktro, et celle qui devait la précéder sur Amiga 1200, ne tournaient dans la trame que du fait d'une erreur de configuration de WinUAE. L'émulation n'était pas fidèle, le hardware ne volant pas autant de cycles au MC68000 que dans la réalité.
Dans Scoopex "TWO", le problème fut résolu par downsizing. Restait à trouver une solution pour Scoopex "ONE". C'est à l'occasion de la programmation d'une BBS-intro à venir pour le groupe Desire qu'elle fut trouvée. Voici donc le détail du coding-of de Scoopex "ONE", une cracktro pour Amiga 1200 :
Cette cracktro exploite quelques possibilités offertes par le chipset AGA (Advanced Graphics Architecture) : l'affichage en 256 couleurs, et le mode "burst" permettant au hardware de lire les données des bitplanes par paquets de 64 bits. En tant que telle, cette cracktro constitue une bonne introduction à la programmation du hardware de l'Amiga 1200, pour ceux qui souhaitent renouer avec le passé de la plus glorieuse gamme de micro-ordinateurs.
Cette cracktro n'a toujours pas été utilisée par Scoopex, mais j'ai jugé qu'après des mois d'attente, il était nécessaire... de ne plus attendre. A priori, elle devrait être utilisée pour la release d'une version AGA de Hired Guns. On verra bien...
| A écouter en lisant l'article... |
Cliquez ici pour télécharger l'intégralité du code et des données de la cracktro.
Cette archive contient les fichiers suivants :
| scoopexONEv6.adf | L'image d'une disquette autoboot pour tester la cracktro | scoopexONEv6.s | le source de la cracktro | common/ptplayer | Le source du player de module | common/debug.s | Le source de routines de débogage | common/interpolate.s | Le source de l'interpolateur linéraire | common/printer.s | Le source du printer | common/registers.s | La définition des constantes des registres hardware | common/wait.s | Le source de l'attente du raster | data/fontWobbly8x8x1.raw | La police en RAW | data/scoopexONESkull320x152x1.raw | L'image en RAW | data/scoopexONELogo320x64x4.raw | Le logo en RAW | data/smash9.mod | Le module |
Comme toujours, vous devrez utiliser un émulateur tel WinUAE et un outil tel que ASM-One pour assembler et exécuter le code. Reportez-vous à cet article pour plus d'explications.
L'apparition du logo
Le logo est une image de 320 x 64 pixels, en 16 couleurs, soit 4 bitplanes. Il est progressivement découvert par des carrés qui vibrent indépendamment les uns des autres. En effet, non seulement ils ne commencent pas à vibrer simultanément, mais lorsqu'ils commencent à vibrer, ils ne sont pas en phase.
La vibration est une animation cyclique où le côté d'un carré de 8 x 8 diminue de 2 pixels à chaque étape, jusqu'à atteindre 0 et s'accroître de 2 pixels à nouveau jusqu'à atteindre sa dimension initiale (spSquareBitmaps) :
Le scénario de révélation d'un carré du logo a fait l'objet d'un certain nombre de tests avant de trouver celui qui ne choque pas l'oeil :
- au départ, le logo - dessiné dans les bitplanes 1 à 4 - est intégralement dissimulé derrière un rectangle noir - dessiné dans le bitplane 6 ;
- apparaît un carré - dessiné dans le bitplane 5 -, dont le côté est nul, mais s'accroît de 2 pixels par étape, produisant un carré blanc qui se dilate sur fond noir ;
- lorsque le côté du carré atteint 8 pixels, le fond noir de ce carré est effacé dans le bitplane 6 ;
- le carré continue son animation cyclique, mais maintenant que le fond noir a été effacé, c'est le logo qui apparaît sur les bords du carré lorsque son côté diminue ;
- au bout d'un certain nombre de cycles (SP_SQUARES_TTL), l'animation du carré s'arrête alors que le côté du carré est nul, révélant totalement le logo sous-jacente.
L'état de chacun des (320 / 8) * (64 / 8) = 320 carrés (spSquaresData) comprend un délai à attendre avant de commencer son animation, et l'image courante de son animation. Les états initiaux sont prédéfinis en utilisant Excel pour générer un délai aléatoire par carré, faute d'intérêt à l'époque pour programmer un PRNG.
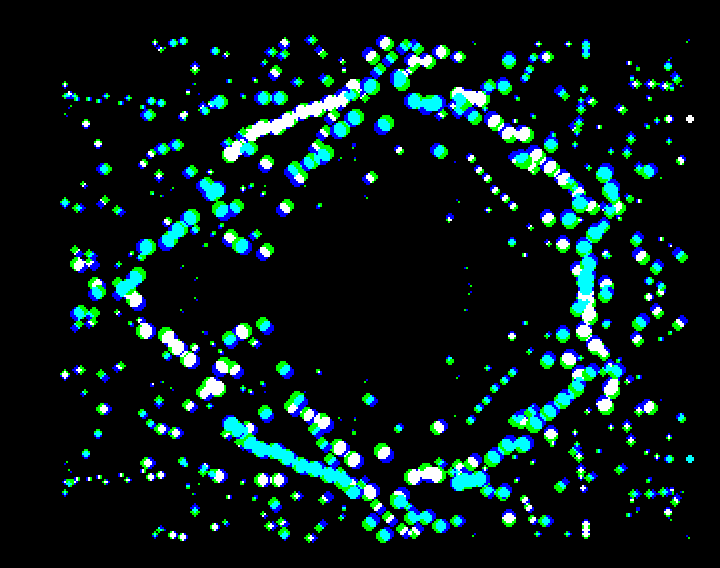
Le résultat produit est ainsi le suivant :
Il serait possible, mais difficile, de calculer le temps pris par l'animation des squares jusqu'à ce que le logo soit totalement révélé. Pour cette raison, Notorious / Scoopex a ajusté empiriquement la musique qu'il a composée une fois la cracktro programmée, de sorte que la fin de la première partie de la musique coïncide bien avec la fin de la révélation du logo.
Le système de particules
Le principal FX dans la cracktro est un système de particules :
Une particule est un objet de 8 x 8 pixels représentant un disque dont le diamètre passe de 8 à 0 pixels en 9 étapes. Cette réduction progressive du diamètre d'un pixel par étape présente l'inconvénient de produire un disque qui oscille dans la surface de l'objet, mais cela est très peu perceptible par le spectateur quand l'objet est en mouvement.
Et en mouvement, il l'est.
Une particule est créée par un générateur, représenté à l'écran comme une particule qui n'est pas animée - un disque de 8 pixels de diamètre. Il y a PARTICLE_SEEDS générateurs, répartis à intervalles réguliers le long d'une trajectoire précalculée de PATH_LENGTH positions. Cette trajectoire est de type système d'équations paramétriques comme une courbe de Lissajous.
Un générateur crée une particule toutes les PARTICLE_DELAY trames. La particule apparaît à la position qu'occupe alors le générateur. Elle se déplace selon un vecteur directeur dont les coordonnées sont simplement la différence entre les coordonnées de la position du générateur et sa position précédente. Pour éviter que des particules générées à haute fréquence n'adoptent des trajectoires trop similaires, ces coordonnées sont légèrement brouillées par l'ajout aléatoire d'un constante empiriquement déterminée (2), en fonction des positions horizontale et verticale du raster au moment de la génération. Par la suite, ces coordonnées ne changent que lorsque la particule atteint un bord, la particule rebondissant sur ce dernier. La vitesse de la particule est initialement PARTICLE_SPEED.
Comment calculer la nouvelle position d'une particule à chaque trame ? Le MC68020 est certainement plus rapide que le MC68000 pour effectuer des multiplications et des divisions, Toutefois, dans la lignée du travail accompli sur Amiga 500, il n'était pas question de recourir à de telles opérations ici. La position de la particule est calculée en s'appuyant sur un algorithme très simple, qui permet de diviser deux valeurs entières à l'aide de seules additions et soustractions, en procédant comme s'il s'agissait de tracer une droite à base de pixels. Cet algorithme est le même que celui évoqué dans l'article sur Scoopex "TWO" - présenté alors comme l'algorithme de Lucas, mais cet algorithme est si peu documenté sur le Web, et il partage tant avec celui de Bresenham, que je ne suis plus certain de pouvoir l'identifier ainsi...
Il est clair que le vecteur directeur de la particule est une approximation - parfois très grossière - de celui de la tangente à la trajectoire du générateur à la position qu'occupe le générateur, et il est tout aussi clair que le déplacement de la particule de PARTICLE_SPEED pixels le long de la plus grande dimension de ce vecteur à chaque trame est une approximation - elle aussi, parfois très grossière - d'une vitesse de PARTICLE_SPEED pixels le long de ce vecteur. Toutefois, cela passe bien à l'écran.
Une particule a une durée de vie limitée, fixée à PARTICLE_TTL trames. Tandis qu'elle vieillit, son image dans l'animation progresse et sa vitesse est ralentie, si bien qu'elle est représentée par un disque toujours plus petit qui se déplace toujours plus lentement. In fine, la particule disparaît et sa vitesse atteint 0 au moment où elle expire. Comme lors du calcul de la position, un algorithme permet de procéder à l'interpolation linéaire de l'indice de l'image de la particule, et à l'interpolation linéaire de sa vitesse, sur toute la durée de vie de la particule, à l'aide de seules additions et soustractions.
Le nombre de particules en vie est limité à NB_PARTICLES. Pour parvenir à afficher un tel nombre de particules, PARTICLE_TTL doit donc être fixé à NB_PARTICLES * PARTICLE_DELAY / PARTICLE_SEEDS.
La liste des particules en vie est maintenue sous la forme d'une liste de structures composées des champs suivants :
| OFFSET_PARTICLE_BITMAP | Indice de l'image de la particule dans la liste des images de son animation ptParticleBitmaps |
| OFFSET_PARTICLE_X | Abscisse de la particule |
| OFFSET_PARTICLE_Y | Ordonnée de la particule |
| OFFSET_PARTICLE_SPEED | Vitesse de la particule le long du vecteur directeur |
| OFFSET_PARTICLE_TTL | Durée de vie restante de la particule |
| OFFSET_PARTICLE_INCX0 | Incrément de l'abscisse de la particule le long de la plus grande dimension du vecteur directeur |
| OFFSET_PARTICLE_INCY0 | Incrément de l'ordonnée de la particule le long de la plus grande dimension du vecteur directeur |
| OFFSET_PARTICLE_INCX1 | Incrément de l'abscisse de la particule le long de la plus petite dimension du vecteur directeur |
| OFFSET_PARTICLE_INCY1 | Incrément de l'ordonnée de la particule le long de la plus petite dimension du vecteur directeur |
| OFFSET_PARTICLE_MINDXDY | Minimum des amplitudes en abscisse et en ordonnée du vecteur directeur |
| OFFSET_PARTICLE_MAXDXDY | Maximum des amplitudes en abscisse et en ordonnée du vecteur directeur |
| OFFSET_PARTICLE_ACCUMULATOR | Accumulateur |
A vrai dire, le rôle des champs de cette structure ne se comprend qu'en étudiant le code qui permet de déplacer une particule à chaque trame. Comme il est possible de le constater, si les coordonnées du vecteur directeur sont (DX, DY), la particule progresse du nombre de pixels correspondant à sa vitesse le long de max (DX, DY), et d'un nombre de pixels proportionnel le long de min (DX, DY). Pour simplifier la programmation, des couples d'incréments sont utilisés par une même boucle que DX soit supérieur à DY, ou qu'il lui soit inférieur:
| DX ≥ DY | DX < DY | |
| incX0 | DX ≥ 0 ? 1 : -1 | 0 |
| incY0 | 0 | DY ≥ 0 ? 1 : -1 |
| incX1 | 0 | DY ≥ 0 ? 1 : -1 |
| incY1 | DX ≥ 0 ? 1 : -1 | 0 |
Ce qui donne :
move.w OFFSET_PARTICLE_X(a0),d1 move.w OFFSET_PARTICLE_Y(a0),d2 move.w OFFSET_PARTICLE_ACCUMULATOR(a0),d3 move.w OFFSET_PARTICLE_SPEED(a0),d4 _ptMoveParticleSpeedLoop: add.w OFFSET_PARTICLE_MINDXDY(a0),d3 cmp.w OFFSET_PARTICLE_MAXDXDY(a0),d3 blt _ptMoveParticlesNoAccumlatorOverflow sub.w OFFSET_PARTICLE_MAXDXDY(a0),d3 add.w OFFSET_PARTICLE_INCX1(a0),d1 add.w OFFSET_PARTICLE_INCY1(a0),d2 _ptMoveParticlesNoAccumlatorOverflow: add.w OFFSET_PARTICLE_INCX0(a0),d1 add.w OFFSET_PARTICLE_INCY0(a0),d2 subq #1,d4 bne _ptMoveParticleSpeedLoop move.w d3,OFFSET_PARTICLE_ACCUMULATOR(a0)
Cette liste des structures des particules est prévue pour comprendre jusqu'à NB_PARTICLES entrées. C'est ce qu'on appelle un barillet, c'est-à-dire une liste gérée comme si elle était circulaire, la première entrée étant considérée comme venant après la dernière. Son début est référencé par ptParticlesStart, sa fin par ptParticlesEnd. L'entrée de la première particule en vie est référencée par ptFirstParticle, et celle qui vient après celle de la dernière particule en vie, par ptNextParticle.
Lorsqu'une particule est créée, sa structure est ajoutée à l'entrée référencée par ptNextParticle, et ce pointeur est incrémenté en le faisant reboucler sur ptParticlesStart si jamais il atteint ptParticlesEnd. Ainsi, par construction, les structures des particules sont triées de la plus vieille à la plus jeune à partir de l'entrée référencée par ptFirstParticle.
La liste des particules est visitée à chaque trame pour éliminer les structures des particules dont la durée de vie a expiré. La liste étant triée comme on vient le dire, la manoeuvre consiste simplement à incrémenter ptFirstParticle en le faisant reboucler sur ptParticlesStart si jamais il atteint ptParticlesEnd.
La démultiplication des particules
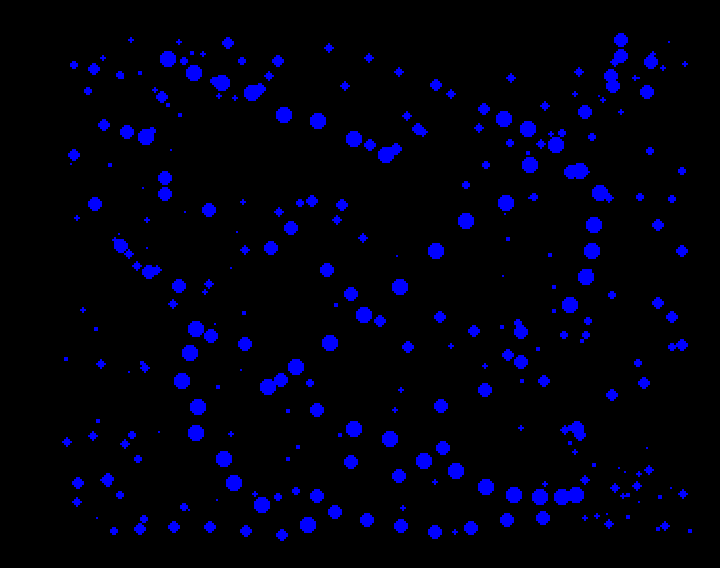
Comme on s'en doute, le nombre de particules visibles à l'écran est de loin supérieur à NB_PARTICULES. En fait, ce nombre est tout simplement quadruplé en recourant à deux techniques : la rémanence et le renversement. En plus de permettre de démultiplier les particules, elles permettent d'en enrichir la palette, qui se limiterait autrement à deux couleurs, dont une pour le fond. Comme il est possible de le constater, le résultat serait alors assez plat :
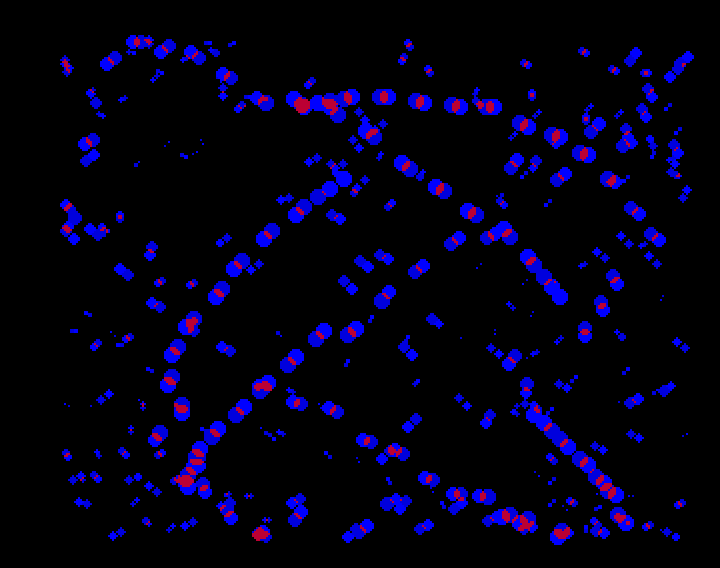
La rémanence consiste à repousser le bitplane contenant l'image qui était affichée à l'arrière, et à dessiner la nouvelle image dans le bitplane qui prend sa place. Ici, à chaque trame T, le précédent bitplane 1 contenant les particules dessinées lors de la trame T-1 devient le bitplane 3, et ls particules sont dessinées dans un nouveau bitplane - qui pourrait être le précédent bitplane 3.
Il en résulte que les particules ne sont plus affichées en une, mais trois couleurs. Une recherche montre qu'utiliser une couleur vive là où les particules des trames T et T+1 se superposent produit un résultat intéressant :
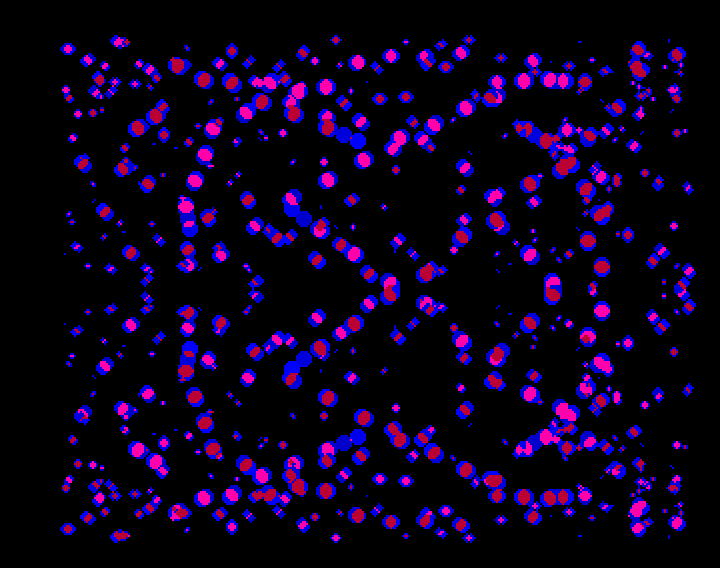
Le reversement consiste à afficher l'image à l'endroit dans un bitplane, et à l'envers dans un autre bitplane, qui se trouve généralement à l'arrière. Pour rappel, pour déterminer l'adresse de départ de la ligne suivante, le hardware ajoute une valeur - le modulo - à l'adresse de fin de la ligne qu'il vient de tracer. Le modulo pouvant être négatif et étant lu dans un registre - BPL1MOD pour les bitplanes impairs, BPL2MOD pour les bitplanes pairs -, cela permet d'afficher des bitplanes impairs à l'envers dans des bitplanes pairs, ou inversement. Ici, les bitplanes 2 et 4 sont les versions reversées des bitplanes 1 et 3, respectivement.
Il en résulte que les particules ne sont plus affichées en trois, mais quinze couleurs. Toutefois, ce nombre est théorique. Une recherche montre que pour donner l'illusion d'une démultiplication des particules, il ne faut pas aider le spectateur à distinguer des les particules des bitplanes 2 et 4 de celles des bitplanes 1 et 3, et donc plutôt généraliser la palette de trois couleurs de ces derniers bitplanes :
La rémanence et la renversement ne prennent aucun temps CPU, puisqu'il s'agit de simplement de modifier quelques mots dans la Copper list - et encore, ce n'est même parfois pas à chaque trame. La démultiplication des particules qui en résulte s'effectue à l'économie. Enfin... il ne faut pas négliger le fait qu'utiliser des bitplanes supplémentaires conduit à voler des cycles pairs, voir impairs, au CPU. On y reviendra.
Au final, l'organisation des bitplanes est la suivante :
| Bitplane | Usage |
| 1 | Particules à l'instant T |
| 2 | Bitplane 1 inversé |
| 3 | Particules à l'instant T-1 |
| 4 | Bitplane 3 inversé |
| 5 | Bitplane 1 du logo, bitplane du texte |
| 6 | Bitplane 2 du logo, bitplane du crâne |
| 7 | Bitplane 3 du logo |
| 8 | Bitplane 4 du logo |
Pour qu'il soit lisible, le texte est affiché au premier plan, masquant tout ce qui se trouve derrière. Par contre, le crâne laisse entrevoir en semi-transparence les particules lorsqu'elles passent derrière. Ces effets sont réalisés en jouant sur certaines couleurs de la palette, éventuellement à partir d'une certaine hauteur dans l'écran, pour réutiliser des couleurs. Par exemple, sous le logo, toutes les couleurs dont le bit 5 est positionné (32, 33, etc.) sont passées à TEXT_COLOR pour afficher le texte, du fait qu'elles ne sont plus utilisées pour afficher le logo qui partage ce bitplane avec le texte.
Comme expliqué ici, le raster a le temps de se déplacer de 8 pixels LowRes tandis que le Copper exécute un MOVE. En conséquence, il faut laisser à ce coprocesseur le temps d'exécuter les MOVE qui modifient les couleurs, avant que le raster ne commence à tracer la ligne où ces couleurs doivent être utilisées. Ici, c'est à partir de la ligne DISPLAY_Y+HALFBRIGHT_Y-2, qui correspond à l'avant-dernière ligne avant celle du séparateur blanc - et non la dernière avant celle du séparateur -, que l'opération doit débuter.
Le printer
Tout à déjà été dit ici sur le printer. En fait, le printer de Scoopex "ONE" est une version antérieure du printer de Scoopex "TWO"
Les transitions
Les transitions sont aussi nécessaires que pénibles à programmer dans une cracktro, et celle-ci, qui fut la première de la série entamée récemment, fut pour moi l'occasion de me le rappeler. Pourquoi ?
- Tout d'abord, le défi technique que cela représente. Il faut parfois passer beaucoup de temps pour trouver le moyen d'intégrer le code la transition au code de la cracktro. Comme le code de la transition doit fonctionner simultanément, il doit se contenter des ressources laissées disponibles, qui peuvent être petitement comptées du fait qu'un FX, qui par définition en consomme beaucoup, est en cours.
- Ensuite, la tâche est particulièrement ingrate. C'est qu'elle ne débouche sur rien de spectaculaire. Quel mérite à faire grandir deux lignes à partir du centre de l'écran jusqu'à ce qu'elles partagent ce dernier en deux, avant d'en déplacer une vers le haut et l'autre vers le bas, pour révéler un fond d'écran à peine visible que du texte vient presque intégralement recouvrir ?
La définition d'une transition est la suivante : c'est un petit rien qui se déroule entre deux grandes choses, l'une qu'elle doit faire décliner, l'autre qu'elle doit faire émerger, et qui n'a pas d'intérêt en soi. Une transition doit faire peu avec des ressources limitées dans un environnement complexe, mais elle doit le faire parfaitement. Délicat...
Burst mode et triple-buffering pour booster les performances
La cracktro exploite huit bitplanes. Quand on sait que sur Amiga 500, passé 4 bitplanes, rajouter des bitplanes conduit à voler des cycles DMA pairs au CPU, on peut se douter qu'une telle profondeur va pénaliser les performances sur Amiga 1200, rétrocomptabilité oblige, conduisant à limiter grandement le nombre de particules. De fait, c'est ce qui s'avère, à moins d'exploiter une fonctionnalité du hardware vidéo qui consiste à lire les données des bitplanes non pas par paquets de 16 pixels, mais par paquets de 64 pixels - une sorte de burst mode, on dira.
A priori, il faudrait que les adresses des bitplanes soient alors alignées sur 64 bits. Du moins, c'est ce qui est requis pour afficher des sprites des 64 pixels de large propres à l'AGA, comme il est possible de le tester à l'aide du code proposé au téléchargement dans cet article - noter le présence de directives CNOP 0,8. Toutefois, en l'espèce, il n'est pas apparu nécessaire de forcer un tel alignement. L'adresse renvoyée par AllocMem () lors de l'allocation en mémoire des bitplanes est utilisée directement sans que cela pose de problème.
Rétrocomptabilité oblige, la lecture par paquets de 64 pixels n'est pas activée par défaut. Pour cela, il faut positionner certains bits dans le registre FMODE propre à l'AGA. Par ailleurs, il faut adapter les valeurs des registres DDFSTRT et DDFSTOP qui spécifient à quel moment le hardware doit commencer à lire et achèver de lire les octets des bitplanes correspondant aux pixels d'une ligne, ainsi que celle des registres des modulos BPL1MOD et BPL2MOD qui spécifient combien d'octets le hardware doit rajouter aux pointeurs sur les bitplanes à la fin de l'affichage d'une ligne. Ainsi, on retrouve dans la Copper list de la cracktro :
move.w #DDFSTRT,(a0)+ move.w #$0038,(a0)+ ;Retrieved by disassembling the Workbench AGA Copper list :) move.w #DDFSTOP,(a0)+ move.w #$00D8,(a0)+ ;Retrieved by disassembling the Workbench AGA Copper list :) move.w #BPL1MOD,(a0)+ move.w #-8,(a0)+ move.w #BPL2MOD,(a0)+ move.w #-8,(a0)+ ;AGA burst mode move.w #FMODE,(a0)+ move.w #$0003,(a0)+
Pour l'anecdote, la référence au désassemblage de la Copper list AGA pour déterminer les valeurs de DFFSTRT et de DDFSTOP est un témoignage de la profonde opacité de ces registres... Certes, l'Amiga Hardware Reference Manual contient bien des explications sur la manière de calculer ces valeurs, mais qui rentre dans le détail réalise bien vite que le raisonnement semble relever d'une abstraction plus que d'une réalité, ce qui le rend difficilement transposable au cas présent. Pour déterminer ces valeurs, j'ai donc désasemblé la Copper list du Workbench après avoir ajusté la résolution à celle de la cracktro :
Retour à la cracktro. Lire les données des bitplanes par paquets de 64 pixels n'est pas la seule technique qui permet de soulager le CPU. Une autre technique, très efficace, employée dans la cracktro consiste à utiliser du triple-buffering plutôt que du double-buffering. Le principe a déjà été expliqué cet article relatif à la réalisation d'un sine scroll sur OCS - la technique n'est pas spécifique à l'AGA. Pour le rappeler brièvement :
- le hardware affiche un premier bitplane contenant l'image N ;
- parallèlement, le CPU dessine l'image N+1 dans un second bitplane ;
- parallèlement, le Blitter efface l'image N-1 dans un troisième bitplane.
Au total, la lecture par paquets de 64 pixels et le triple-buffering permet de relever le nombre maximum de particules affichées de 70 à... 300, donc de passer de 280 à 1 200 particules apparentes grâce aux effets démultiplicateurs décrits plus tôt - rémanence et renversement. C'est tout simplement ce qui a permis de sortir la cracktro des cartons dans lesquels elle avait été laissée.
Le coding-of
L'histoire de cette cracktro remonte à l'été 2017. Parti sur l'idée de produire une démo, je programme plusieurs FX pour Amiga 500, dont une première version du système de particules présenté plus tôt :
L'idée me vient alors de démultiplier le nombre de particules à l'aide des techniques de rémanence et de renversement. Toutefois, il y a un problème : si je mobilise quatre bitplanes pour cela, il ne m'en restera plus qu'un pour un logo, en montant à cinq bitplanes. Sans doute, il serait possible d'utiliser les bitplanes des particules, mais il en découlerait deux contraintes :
- redessiner le logo dans ces bitplanes à chaque trame, ce qui s'effectuerait au détriment du nombre de particules ;
- imposer la palette au graphiste, mais rien ne dit que cela l'enchante vu les couleurs pétantes, et il est déjà assez difficile d'en trouver un.
En conséquence, je décide de cibler l'Amiga 1200, donc de passer de l'OCS à l'AGA. Sur cette machine, je disposerai de huit bitplanes, ce qui sera parfait pour ménager la possibilité d'afficher un logo en 16 couleurs par dessus les particules.
Chose faite, je fais parvenir à la cracktro à Galahad, qui me remercie tout en m'indiquant qu'aucune release de jeu AGA n'est pour l'heure prévue. Par contre, il s'apprête à sortir le portage d'un jeu ST sur Amiga 500. Si donc le coeur m'en dit, une cracktro pour OCS est bienvenue. C'est l'histoire de Scoopex "TWO", précédemment narrée ici.
Comme rapporté dans ce récit, au moment de la diffusion de Scoopex "TWO", je constate que du fait d'une erreur de configuration de WinUAE, cette cracktro ne tourne pas dans la trame. L'émulation n'est pas fidèle, le hardware ne volant pas autant de cycles au MC68000 que dans la réalité. Tout se passe comme si j'avais surestimé les capacités de calcul de l'Amiga.
Comme j'ai programmé Scoopex "ONE" avant, je réalise que le problème affecte aussi cette cracktro. Une fois WinUAE correctement configuré, le nombre maximum de particules qu'il est possible d'afficher dans la trame chute vertigeusement de plus de 500 à guère plus de 70. Dans ces conditions, le FX n'a plus rien d'impressionnant, et Scoopex "TWO" ne peut donc être distribuée sans risquer la honte. Une chance qu'à l'époque, Galahad n'a pas eu de release AGA en attente de cracktro, car il avait visiblement commis la même erreur d'appréciation que moi...
Il faut trouver une solution ou enterrer le code. Toutefois, je suis déjà engagé sur la programmation d'autres petites choses - notamment "Scoopex THREE", un menu de trainer pour StingRay. Je laisse donc filer, en me disant que j'y reviendrai un jour... ou jamais ! Car sur le moment, je dois bien avouer que je ne vois pas très bien comment faire mieux.
Longtemps après, je dois me frotter à l'AGA pour expliquer comment afficher des sprites de 64 pixels de large en 256 couleurs dans le cadre de la rédaction d'un article sur ces hobbits du hardware vidéo. C'est alors que je me souviens - ce qui est un comble, car j'étais quand l'un de ceux qui avaient commencé à le documenter à l'époque - que l'AGA peut afficher de tels sprites en utilisant une lecture accélérée des données en mémoire vidéo.
L'exploration de la documentation officieuse de l'AGA - comme je l'ai expliqué, Commodore n'a jamais documenté officiellement ce hardware - me renseigne sur le fait qu'il en va de même pour les bitplanes. Je fais le pari raisonnable que cela peut libérer des cycles pour le CPU, et donc me permettre d'accroître le nombre de particules. Je teste, et il s'avère que c'est bien le cas.
Le gain est là, mais il reste limité au regard du nombre de particules d'où je suis parti. Pour l'accroître plus encore, je décide dans la foulée de mobiliser la technique du triple-buffering que j'avais à l'époque écartée, par flegme. Cela me contraint de réécrire une petite partie du code. Rien de bien de grave quand je peux constater qu'au final, cette technique jointe à l'autre me permet d'atteindre un nombre de particules beaucoup plus conséquent, et de produire un effet à l'écran proche de celui auquel j'étais tout d'abord parvenu.
La cracktro est sauvée. Elle pourra être jouée sur les écrans de petits et grands. Ouf !
Et voilà !
Nul doute qu'il est possible de faire mieux en assembleur avec le chipset AGA. Toutefois, le système de particules est assez sympa - même s'il serait possible d'en démontrer la puissance autrement qu'en faisant simplement circuler les générateurs le long d'une trajectoire précalculée. Et finalement, les magnifiques graphismes et l'excellente musique rehaussent l'ensemble, pour en faire quelque chose qui se tient.
Pas de cracktro digne de ce nom sans credits et greetings. Pour les premiers :
- Code par votre serviteur ;
- Image par Alien / Paradox ;
- Musique par Notorious / Scoopex.
Pour les seconds, je renvoie aux pages de la cracktro. Néanmoins, je tiens à remercier tout particulièrement Galahad / Scoopex, qui m'a motivé en m'offrant l'opportunité de diffuser cette cracktro... en attendant qu'elle le soit un jour !