Comment calculer les coordonnées des points formant une enveloppe régulière d'un polygone quelconque, c'est-à-dire une version plus grande ou plus petite du polygone qui semble parfaitement s'emboîter avec ce dernier (enveloppe homothétique) ? :
Le parfait emboîtage de l'enveloppe et du polygone tient au fait que la distance entre un sommet du polygone et le sommet correspondant de l'enveloppe est constante.
Calculer les coordonnées des sommets de l'enveloppe par simple application d'un facteur d'agrandissement aux coordonnées des sommest du polygone ne permet pas de parvenir au résultat souhaité. En effet, un tel facteur ne pourrait s'appliquer qu'autour d'un centre, c'est-à-dire un point qui devrait se trouver à égale distance de tous les sommets du polygone pour entraîner un éloignement ou un rapprochement de la distance attendue des sommets correspondants de l'enveloppe.
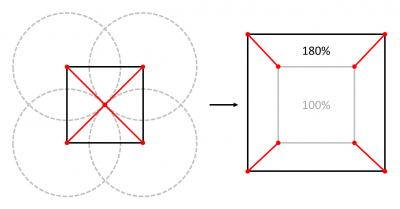
Or l'existence d'un ensemble de cercles de même rayon, centrés sur chacun des sommets du polygone, qui se recoupent en un unique point constituant ce centre, n'a rien de systématique. En fait, ce n'est le cas que pour des polygones très particuliers :
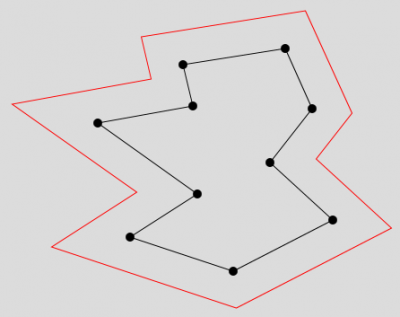
Dans les autres cas, on constate en pratique qu'il est impossible de trouver ce jeu de cercles qui se recoupent en un même point. Ainsi, sur cet exemple, il serait impossible de positionner l'enveloppe résultant de la simple application d'un facteur d'agrandissement de sorte que les sommets de l'enveloppe se trouvent même à une distance constante des sommets du polygone auxquels ils correspondent :
La solution
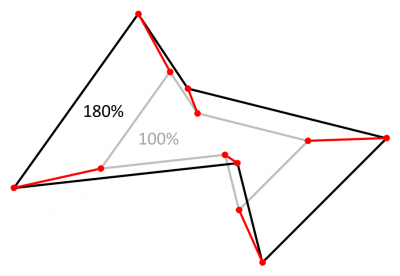
Ce n'est pas le long d'un axe partant d'un centre et rejoignant le sommet d'un polygone qu'il faut déplacer ce sommet pour déterminer le sommet correspondant de l'enveloppe. C'est le long d'un axe qui est celui de la normale au polygone en ce sommet.
La normale en un sommet d'un polygone est définie comme la somme normalisée des normales aux deux côtés issus de ce sommet. Après avoir calculé cette normale, il suffit d'appliquer une translation au sommet pour le positionner à la distance souhaitée de l'enveloppe au polygone.
Le code JavaScript
En JavaScript, la solution se traduit par le code suivant :
/*------------------------------------------------------------------------------
Retourne les points composant l'enveloppe d'un polygone à une certaine distance de ce dernier.
ENTREE
points Tableau des points {x, y} dans le sens des aiguilles d'une montre
d Distance de l'enveloppe au polygone
round Arrondir les valeurs retournées
SORTIE
Tableau des points {x, y} composant l'enveloppe (externe si les points étaient donnés dans le sens trigonométrique, interne sinon).
-----------------------------------------------------------------------------*/
function hull (points, d, round) {
var hull, i, xA, yA, xB, yB, xC, yC, AB, BC, xI, yI, k, xM, yM;
if (points.length < 3)
return (null);
hull = new Array ();
points.push (points[0]);
xA = points[points.length - 2].x;
yA = points[points.length - 2].y;
xB = points[0].x;
yB = points[0].y;
AB = Math.sqrt ((xB - xA) * (xB - xA) + (yB - yA) * (yB - yA));
i = 1;
while (true) {
xC = points[i].x;
yC = points[i].y;
BC = Math.sqrt ((xC - xB) * (xC - xB) + (yC - yB) * (yC - yB));
xI = 0.5 * ((yA - yB) / AB + xB - (yC - yB) / BC + xB);
yI = 0.5 * (- (xA - xB) / AB + yB + (xC - xB) / BC + yB);
k = d / ((xI - xB) * (xI - xB) + (yI - yB) * (yI - yB));
xM = k * (xI - xB) + xB;
yM = k * (yI - yB) + yB;
if (round)
hull.push ({x:Math.round (xM), y:Math.round (yM)});
else
hull.push ({x:xM, y:yM});
i ++;
if (i == points.length)
break;
xA = xB;
yA = yB;
xB = xC;
yB = yC;
AB = BC;
}
points.pop ();
return (hull);
}
L'exemple
Cliquez ici pour accéder à une page de test minimaliste. Vous pourrez visualiser le code et le récupérer pour travailler avec.
Les maths
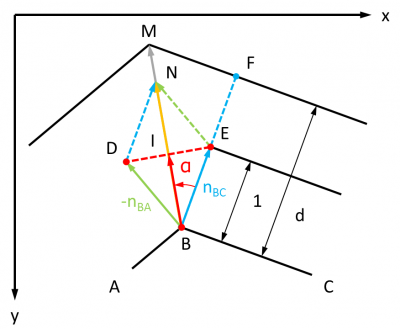
Le point de départ est l'écriture de cos (α) :
cos (α) = BI / BE = BF / BM
D'où :
BM = BF * BE / BI = d * 1 / BI = d / BI
La colinéarité entre les vecteurs dit qu'entre les vecteurs BM et BN :
BM = k * BN
Avec :
k = BM / BI = d / BI2
D'où :
- xM = k * (xN - xB) + xB
- yM = k (yN - yB) + yB
Quant au calcul de xM et yM, nous avons déjà vu comment calculer la normale en un angle d'un polygone...