Tout développeur qui s'initie à la 3D avec WebGL est rapidement confronté à une entité mathématique, la matrice de projection :

$\left[\begin{array}{cccc}\mathrm{X<msub>e</msub>}& \mathrm{Y<msub>e</msub>}& \mathrm{Z<msub>e</msub>}& 1\end{array}\right]x\left[\begin{array}{cccc}\frac{2N}{R-L}& 0& 0& 0\\ 0& \frac{2N}{T-B}& 0& 0\\ \frac{R+L}{R-L}& \frac{T+B}{T-B}& \frac{F+N}{N-F}& \mathrm{<mo>-</mo>1}\\ 0& 0& \frac{2FN}{N-F}& 0\end{array}\right]$

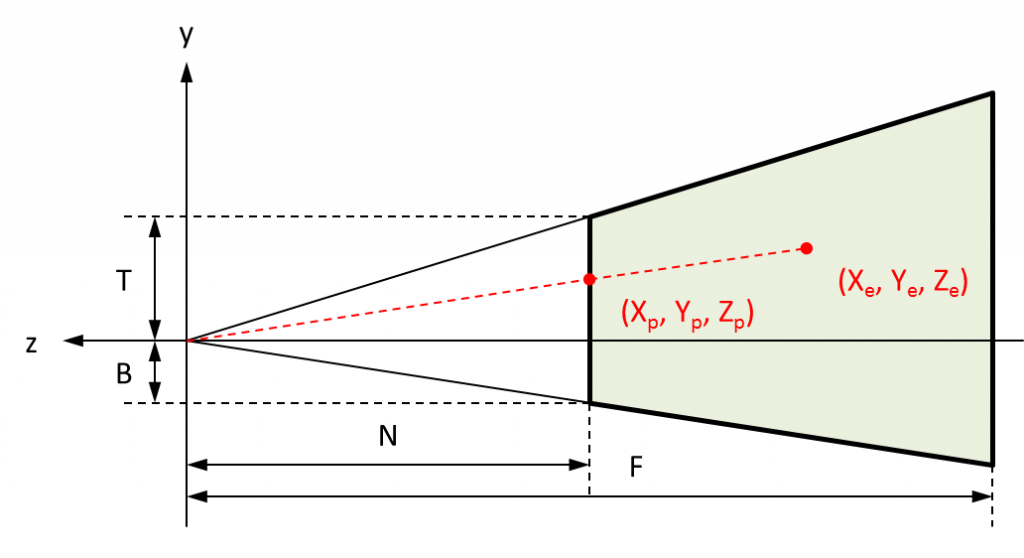
Les différentes constantes utilisées pour définir le volume de clipping se présentant par exemple ainsi (coupe Y/Z) :

Cette matrice peut sembler d'autant plus étrange au développeur qu'elle comporte 4 lignes et 4 colonnes (une matrice 4x4), alors qu'il semblerait que l'on puisse se contenter d'une matrice 3x3 pour réaliser les calculs. D'ailleurs, où est passée l'intervention de $\mathrm{Z<msub>e</msub>}$ au dénominateur dans les calculs ?

Bref, pourquoi cette matrice ? Comment calculer ses coefficients ? Et comment en déduire les coordonnées de la projection d'un point ?

A écouter en lisant l'article...

Soit le point $(\mathrm{X<msub>e</msub>},\mathrm{Y<msub>e</msub>},\mathrm{Z<msub>e</msub>})$. Le principe des coordonnées homogènes est qu'au terme de la multiplication d'une matrice $\left[\begin{array}{cccc}\mathrm{X<msub>e</msub>}& \mathrm{Y<msub>e</msub>}& \mathrm{Z<msub>e</msub>}& 1\end{array}\right]$ par une matrice 4x4 de projection, on obtienne une matrice $\left[\begin{array}{cccc}\mathrm{X<msub>c</msub>}& \mathrm{Y<msub>c</msub>}& \mathrm{Z<msub>c</msub>}& 1\end{array}\right]$ telle que $(\frac{\mathrm{X<msub>c</msub>}}{\mathrm{W<msub>c</msub>}},\frac{\mathrm{Y<msub>c</msub>}}{\mathrm{W<msub>c</msub>}},\frac{\mathrm{Z<msub>c</msub>}}{\mathrm{W<msub>c</msub>}})$ constituent les versions normalisées des coordonnées la projection du point $(\mathrm{X<msub>p</msub>},\mathrm{Y<msub>p</msub>},\mathrm{Z<msub>p</msub>})$ :

$-1\le \frac{\mathrm{X<msub>c</msub>}}{\mathrm{W<msub>c</msub>}}\le 1$	si	$L\le \mathrm{X<msub>p</msub>}\le R$
$-1\le \frac{\mathrm{Y<msub>c</msub>}}{\mathrm{W<msub>c</msub>}}\le 1$	si	$B\le \mathrm{Y<msub>p</msub>}\le T$
$-1\le \frac{\mathrm{Z<msub>c</msub>}}{\mathrm{W<msub>c</msub>}}\le 1$	si	$N\le -\mathrm{Z<msub>e</msub>}\le F$

Sans aller jusqu'à dire que recourir à des coordonnées homogènes ne soit justifié que par cela, il faut noter que cette matrice présente deux intérêts :

• Tout d'abord, tous ses éléments sont indépendants des coordonnées du point, puisque la division par une grandeur dépendant de $\mathrm{Z<msub>e</msub>}$, sans laquelle aucune projection ne serait possible, est repoussée à une étape ultérieure. Dans ces conditions, il sera possible de projeter une série de points après avoir calculé les coefficients de la matrice une seule fois.
• Ensuite, le résultat de la multiplication par la matrice suivi de la division par $\mathrm{W<msub>c</msub>}$ sera normalisé. Pourquoi normaliser ? Car cela permettra de savoir rapidement si le point transformé se trouvait dans le volume de clipping. Si au moins une des coordonnées de sa projection ne respecte pas les inégalités correspondantes, le point était en dehors ce volume, ce qui doit entraîner découpage et/ou exclusion des surfaces dont il est un sommet.

Pour rappel, le volume de clipping n'est pas un cube : c'est une pyramide tronquée. En effet, il faut bien noter que les inégalités concernent $\mathrm{X<msub>p</msub>}$ et $\mathrm{Y<msub>p</msub>}$, et non $\mathrm{X<msub>e</msub>}$ et $\mathrm{Y<msub>e</msub>}$. En imposant des contraintes sur les coordonnées de la projection du point et non du point, on signifie bien que seuls les points dont les projections tiennent dans la surface de projection, et qui se trouvent entre telle et telle profondeur, doivent pouvoir être retenu pour l'affichage en testant de simples inégalités au terme des calculs.

Pourquoi $-\mathrm{Z<msub>e</msub>}$ ? Car dans WebGL, l'axe des affixes est orienté vers l'observateur, qui est positionné à son origine. Le plan de projection est confondu avec le plan de clipping avant (situé à une distance $N$, exprimée positivement). Le plan de clipping arrière est situé à une distance $F$ de l'observateur (exprimée aussi positivement).

La question est de savoir quels doivent être les éléments de la matrice 4x4 sachant que (on le répète), ils doivent être totalement indépendants des coordonnées $(\mathrm{X<msub>e</msub>},\mathrm{Y<msub>e</msub>},\mathrm{Z<msub>e</msub>})$.

Pour faciliter la lecture, posons que la matrice des coordonnées $\left[\begin{array}{cccc}\mathrm{X<msub>e</msub>}& \mathrm{Y<msub>e</msub>}& \mathrm{Z<msub>e</msub>}& 1\end{array}\right]$ est un vecteur ligne. La matrice 4x4 recherchée est :

$\left[\begin{array}{cccc}\mathrm{A<msub>x</msub>}& \mathrm{B<msub>x</msub>}& \mathrm{C<msub>x</msub>}& \mathrm{D<msub>x</msub>}\\ \mathrm{A<msub>y</msub>}& \mathrm{B<msub>y</msub>}& \mathrm{C<msub>y</msub>}& \mathrm{D<msub>y</msub>}\\ \mathrm{A<msub>z</msub>}& \mathrm{B<msub>z</msub>}& \mathrm{C<msub>z</msub>}& \mathrm{D<msub>z</msub>}\\ \mathrm{A<msub>w</msub>}& \mathrm{B<msub>w</msub>}& \mathrm{C<msub>w</msub>}& \mathrm{D<msub>w</msub>}\end{array}\right]$

Par exemple, on a donc :

$\mathrm{X<msub>c</msub>}=\mathrm{A<msub>x</msub>}\mathrm{X<msub>e</msub>}+\mathrm{A<msub>y</msub>}\mathrm{Y<msub>e</msub>}+\mathrm{A<msub>z</msub>}\mathrm{Z<msub>e</msub>}+\mathrm{A<msub>w</msub>}$

En appliquant le théorème de Thalès, on détermine que :

$\frac{\mathrm{X<msub>p</msub>}}{\mathrm{X<msub>e</msub>}}=\frac{N}{-\mathrm{Z<msub>e</msub>}}$

$\mathrm{X<msub>p</msub>}=\frac{N}{-\mathrm{Z<msub>e</msub>}}\mathrm{X<msub>e</msub>}$

Partons du résultat. On souhaite finalement que si... (1) :

$L\le \mathrm{X<msub>p</msub>}\le R$

...on calcule en fait $\frac{\mathrm{X<msub>c</msub>}}{\mathrm{W<msub>c</msub>}}$, version normalisée de $\mathrm{X<msub>p</msub>}$, telle que :

$-1\le \frac{\mathrm{X<msub>c</msub>}}{\mathrm{W<msub>c</msub>}}\le 1$

Donc :

$-\mathrm{W<msub>c</msub>}\le \mathrm{A<msub>x</msub>}\mathrm{X<msub>e</msub>}+\mathrm{A<msub>y</msub>}\mathrm{Y<msub>e</msub>}+\mathrm{A<msub>z</msub>}\mathrm{Z<msub>e</msub>}+\mathrm{A<msub>w</msub>}\le \mathrm{W<msub>c</msub>}$

Partons de (1). Il se trouve que rapporter une valeur $\mathrm{V}$ de l'intervalle $[L,R]$ à l'intervalle $[-1,1]$ est assez simple :

$\begin{array}{ccccc}L& \le & \mathrm{V}& \le & R\\ 0& \le & V-L& \le R-L\\ 0& \le & \frac{V-L}{R-L}& \le & 1\\ 0& \le & \frac{2(V-L)}{R-L}& \le & 2\\ -1& \le & \frac{2(V-L)}{R-L}-1& \le & 1\\ -1& \le & \frac{2V-R-L}{R-L}& \le & 1\end{array}$

Donc si $V=\mathrm{X<msub>p</msub>}=\frac{N}{-\mathrm{Z<msub>e</msub>}}\mathrm{X<msub>e</msub>}:$

$\begin{array}{ccccc}-1& \le & \frac{\frac{2N}{-\mathrm{Z<msub>e</msub>}}\mathrm{X<msub>e</msub>}-R-L}{R-L}& \le & 1\\ -1& \le & \frac{2N}{-\mathrm{Z<msub>e</msub>}(R-L)}\mathrm{X<msub>e</msub>}-\frac{R+L}{R-L}& \le & 1\end{array}$

A partir de là, si $\mathrm{Z<msub>e</msub>}\le 0$ (ce qui correspond bien à la situation, comme il est possible de le constater sur la figure au début de cet article, la pyramide tronquée résidant dans les affixes négatives), alors il est possible de multiplier par $-\mathrm{Z<msub>e</msub>}\ge 0$ sans inverser les inégalités :

$\mathrm{Z<msub>e</msub>}\le \frac{2N}{R-L}\mathrm{X<msub>e</msub>}+\frac{R+L}{R-L}\mathrm{Z<msub>e</msub>}\le -\mathrm{Z<msub>e</msub>}$

C'est une couple d'inégalités de la forme qu'on recherche :

$-\mathrm{W<msub>c</msub>}\le \mathrm{A<msub>x</msub>}\mathrm{X<msub>e</msub>}+\mathrm{A<msub>y</msub>}\mathrm{Y<msub>e</msub>}+\mathrm{A<msub>z</msub>}\mathrm{Z<msub>e</msub>}+\mathrm{A<msub>w</msub>}\le \mathrm{W<msub>c</msub>}$

A condition donc de poser que $\mathrm{W<msub>c</msub>}=-\mathrm{Z<msub>e</msub>}$.

Partant, les calculs peuvent être inscrits dans la matrice :

$\left[\begin{array}{c}\mathrm{A<msub>x</msub>}\\ \mathrm{A<msub>y</msub>}\\ \mathrm{A<msub>z</msub>}\\ \mathrm{A<msub>w</msub>}\end{array}\right]=\left[\begin{array}{c}\frac{2N}{R-L}\\ 0\\ \frac{R+L}{R-L}\\ 0\end{array}\right]$

Sans oublier :

$\left[\begin{array}{c}\mathrm{D<msub>x</msub>}\\ \mathrm{D<msub>y</msub>}\\ \mathrm{D<msub>z</msub>}\\ \mathrm{D<msub>w</msub>}\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ -1\\ 0\end{array}\right]$

Même raisonnement que pour les coefficients pour calculer $\mathrm{X<msub>c</msub>}$, ce qui débouche sur :

$\left[\begin{array}{c}\mathrm{B<msub>x</msub>}\\ \mathrm{B<msub>y</msub>}\\ \mathrm{B<msub>z</msub>}\\ \mathrm{B<msub>w</msub>}\end{array}\right]=\left[\begin{array}{c}0\\ \frac{2N}{T-B}\\ \frac{T+B}{T-B}\\ 0\end{array}\right]$

On sait désormais que $\mathrm{W<msub>c</msub>}=-\mathrm{Z<msub>e</msub>}$ et on n'y veut rien changer, car ce serait remettre en cause les calculs précédents. On souhaite que si... :

$N\le -\mathrm{Z<msub>e</msub>}\le F$

...alors :

$-1\le \frac{\mathrm{Z<msub>c</msub>}}{\mathrm{W<msub>c</msub>}}\le 1$

Comme $\mathrm{X<msub>c</msub>}$ et $\mathrm{Y<msub>c</msub>}$, $\mathrm{Z<msub>c</msub>}$ prend la forme d'une combinaison linéaire de $\mathrm{X<msub>e</msub>}$, $\mathrm{Y<msub>e</msub>}$ et $\mathrm{Z<msub>e</msub>}$ :

$\mathrm{Z<msub>c</msub>}=\mathrm{C<msub>x</msub>}\mathrm{X<msub>e</msub>}+\mathrm{C<msub>y</msub>}\mathrm{Y<msub>e</msub>}+\mathrm{C<msub>z</msub>}\mathrm{Z<msub>e</msub>}+\mathrm{C<msub>w</msub>}$

On ne va surtout pas s'emmerder en rendant $\mathrm{Z<msub>c</msub>}$ dépendant de $\mathrm{X<msub>e</msub>}$ et de $\mathrm{Y<msub>e</msub>}$, car on ne voit pas du tout ce que cela pourrait apporter ($\mathrm{Z<msub>e</msub>}$ est totalement indépendant de $\mathrm{X<msub>e</msub>}$ et $\mathrm{Y<msub>e</msub>}$ !). On va donc d'emblée poser que :

$\mathrm{C<msub>x</msub>}=0$

$\mathrm{C<msub>y</msub>}=0$

Bref :

$\mathrm{Z<msub>c</msub>}=\mathrm{C<msub>z</msub>}\mathrm{Z<msub>e</msub>}+\mathrm{C<msub>w</msub>}$

Ainsi, le problème se résume à déterminer $\mathrm{C<msub>z</msub>}$ et $\mathrm{C<msub>w</msub>}$, indépendants de $\mathrm{X<msub>e</msub>}$, $\mathrm{Y<msub>e</msub>}$ et $\mathrm{Z<msub>e</msub>}$, et tels que si $-\mathrm{Z<msub>e</msub>}$ est dans $[N,F]$, alors :

$-1\le \frac{\mathrm{C<msub>z</msub>}\mathrm{Z<msub>e</msub>}+\mathrm{C<msub>w</msub>}}{\mathrm{W<msub>c</msub>}}\le 1$

Sachant que $\mathrm{W<msub>c</msub>}=-\mathrm{Z<msub>e</msub>}$, on peut donc développer :

$\begin{array}{ccccc}-1& \le & -\mathrm{C<msub>z</msub>}-\frac{\mathrm{C<msub>w</msub>}}{\mathrm{Z<msub>e</msub>}}& \le & 1\\ \mathrm{C<msub>z</msub>}-1& \le & \frac{-\mathrm{C<msub>w</msub>}}{\mathrm{Z<msub>e</msub>}}& \le & \mathrm{C<msub>z</msub>}+1\end{array}$

A ce stade, il faut faire un choix. En effet, puisqu'il s'agit de diviser par $\mathrm{C<msub>w</msub>}$, faut-il considérer qu'il s'agit d'un nombre positif ou négatif ? Dans le premier cas, les inégalités sont conservées ; dans le second, elles sont inversées.

Je n'ai pas trouvé de solution plus rationnelle que de poursuivre les calculs dans l'un et l'autre cas, pour retenir la solution qui convient. C'est très bête. Si quelqu'un trouve mieux, ce qui est définitivement possible, qu'il me le fasse savoir en passant par la page Contact.

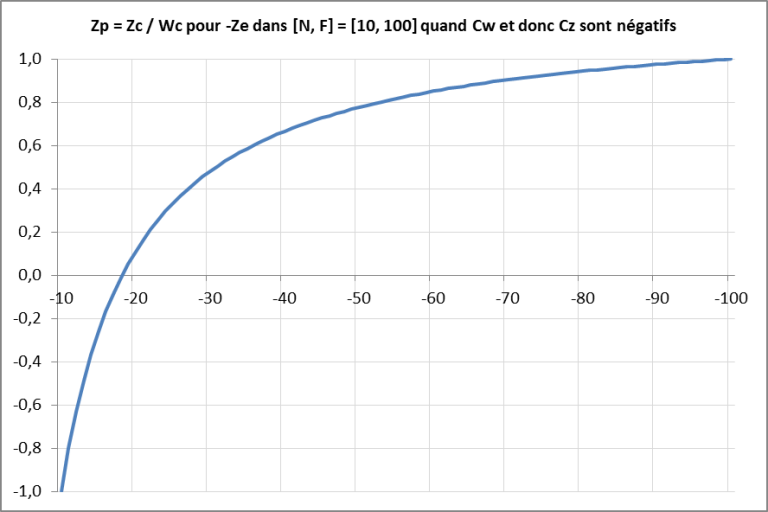
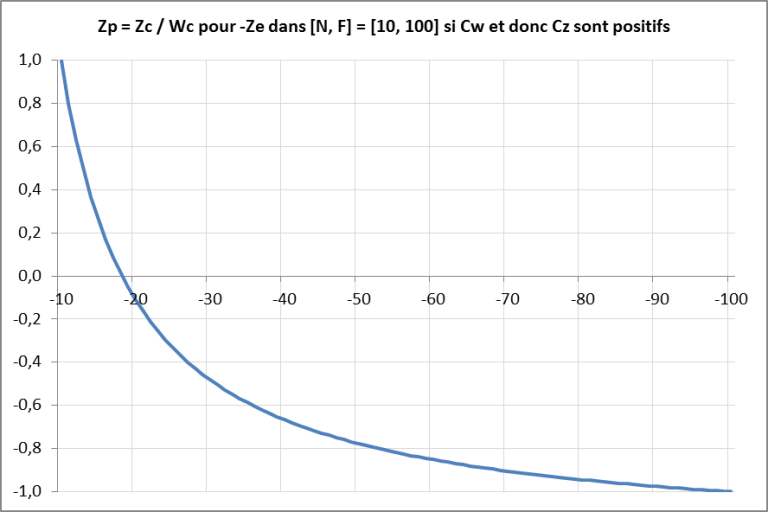
Un test d'une matrice de transformation dans Excel à récupérer ici permet de produire ces deux courbes rendant compte de l'évolution de $\frac{\mathrm{Z<msub>c</msub>}}{\mathrm{W<msub>c</msub>}}$ quand $\mathrm{Z<msub>e</msub>}$ évolue entre $-N$ et $-F$ :

C'est donc la solution $\mathrm{C<msub>w</msub>}\le 0$ qu'il faut retenir. En divisant par $\mathrm{C<msub>w</msub>}$, les inégalités sont donc inversées. Les calculs se poursuivent ainsi :

$\begin{array}{ccccc}\frac{\mathrm{C<msub>z</msub>}-1}{\mathrm{C<msub>w</msub>}}& \ge & \frac{-1}{\mathrm{Z<msub>e</msub>}}& \ge & \frac{\mathrm{C<msub>z</msub>}+1}{\mathrm{C<msub>w</msub>}}\\ \frac{\mathrm{C<msub>w</msub>}}{\mathrm{C<msub>z</msub>}-1}& \le & -\mathrm{Z<msub>e</msub>}& \le & \frac{\mathrm{C<msub>w</msub>}}{\mathrm{C<msub>z</msub>}+1}\end{array}$

Or ces inégalités doivent se constater quand $N\le -\mathrm{Z<msub>e</msub>}\le F$. On peut donc poser que :

$F=\frac{\mathrm{C<msub>w</msub>}}{\mathrm{C<msub>z</msub>}+1}$

$N=\frac{\mathrm{C<msub>w</msub>}}{\mathrm{C<msub>z</msub>}-1}$

C'est un système de deux égalités à deux inconnues, qui se résout en injectant la première dans la seconde :

$N=\frac{F(\mathrm{C<msub>z</msub>}+1)}{\mathrm{C<msub>z</msub>}-1}$

$N(\mathrm{C<msub>z</msub>}-1)=F(\mathrm{C<msub>z</msub>}+1)$

$\mathrm{C<msub>z</msub>}(N-F)=F+N$

$\mathrm{C<msub>z</msub>}=\frac{F+N}{N-F}$

Donc en injectant ce résultat dans la première (ou la seconde, c'est pareil) :

$F=\frac{\mathrm{C<msub>w</msub>}}{\frac{F+N}{N-F}+1}$

$\mathrm{C<msub>w</msub>}=\frac{F(F+N)}{N-F}+F$

$\mathrm{C<msub>w</msub>}=\frac{F(F+N)+F(N-F)}{N-F}$

$\mathrm{C<msub>w</msub>}=\frac{2FN}{N-F}$

C'est fini !

Il faut noter que dans WebGL, la matrice des coordonnées est un vecteur colonne et non ligne. En conséquence, il faut procéder à une transposition :

Comme on peut le constater, les calculs sont guidés par le souci de trouver des coefficients dans la matrice qui sont indépendants de $\mathrm{X<msub>e</msub>}$, $\mathrm{Y<msub>e</msub>}$ et $\mathrm{Z<msub>e</msub>}$.

Cela faisait fort longtemps que je voulais tirer au clair la manière dont la matrice de projection 4x4 est construite. En 1999, j'ai publié un ouvrage Direct3D, 3D temps réel sous Windows. A l'époque, j'avais cherché des explications complètes sur la manière de calculer cette matrice pour les reproduire dans les annexes. En vain !

En effet, j'avais pu constater que le calcul de la matrice de projection 4x4 était un de ces sujets que les auteurs présentent sans aller jusqu'au bout, parce que finalement, ils n'ont pas compris - ou ne se sont pas donné la peine de comprendre -, ce dont ils parlent. On tombe parfois sur ce genre de difficulté en lisant un ouvrage technique, et c'est extrêmement frustrant. Par exemple, qu'on me trouve un livre de statistiques relativement abordable qui explique pourquoi on calcule l'écart-type comme il se calcule. Tout le monde semble prendre la formule pour une vérité divine, alors qu'elle a bien été inventée par quelqu'un ! Pénible...

Enfin, pour revenir à cette matrice, je suis tout récemment tombé sur une explication qui répond parfaitement à mes attentes, ici puis ici, sur l'excellent site ScratchPixel 2.0 que je ne saurais trop recommander pour la qualité des explications qu'il contient.

Après avoir survolé les explications données sur ce site, je me suis remis à l'ouvrage en adoptant un angle d'attaque moins rigoureux mais plus intuitif pour moi, aboutissant à cette explication. Il n'est jamais trop tard pour régler ses comptes avec soi-même. Par ailleurs, sa rédaction m'aura donné l'occasion de découvrir MathML pour présenter les équations.

Sur ce point, si quelqu'un sait comment coder correctement le signe négatif pour une variable, c'est-à-dire éviter d'utiliser <mo>-</mo> qui génère un gros signe moins et non un petit (comme il est possible de le faire pour un nombre : utiliser <mn>-1</mn> qui produit un beau $-1$ plutôt que d'utiliser <mo>-</mo><mn>1</mn> qui produit un affreux $-1$), qu'il me le fasse savoir en passant par la page Contact. Firefox ne reconnaît pas <minus/> pour l'heure.