En s'appuyant sur les shaders - le vertex shader (VS) et le fragment shader (FS) - de WebGL, produire une animation de "pixels" s'éloignant d'un point d'origine en tournoyant (autour de leurs centres et autour du centre de l'écran), en grossissant et devenant toujours plus transparents jusqu'à disparaître de l'écran, comme sur la figure suivante qui reprend quatre étapes :

Quatre étapes de l'explosion de "pixels"

WebGL est simple à utiliser. La difficulté réside dans un dilemme auquel le développeur est inévitablement confronté dès qu'il s'attaque à des effets un peu compliqués :

déporter la transformation des points dans les shaders si bien qu'il suffit d'appeler une fois drawElements () pour rendre tous les éléments lors d'une étape de l'animation, mais c'est au prix d'une inflation du buffer des points et d'une mise à jour fréquente de ce dernier ;
déporter la transformation des points dans le programme principal (ie : le programme JavaScript) si bien qu'il est possible de créer une fois pour toutes le buffer des points, mais c'est au prix d'autant d'appels à drawElements () qu'il y a d'éléments à rendre lors d'une étape de l'animation.

Pour être complet, il faut évoquer une troisième solution qui consiste à déporter la transformation des points dans le programme principal, lequel met à jour le buffer des points avec les résultats de cette transformation avant d'appeler une seule fois drawElements (), et ce à chaque étape de l'animation. Toutefois, cette solution doit être écartée, car elle revient à réduire le VS au rang de passe-plat entre le programme principal et le FS puisque le VS est alimenté avec des points déjà transformés. Or si le GPU peut assurer la transformation des points, autant l'utiliser, car cela libère le CPU pour d'autres tâches.

Cet article est le premier d'une série de deux. Il est consacré à la logique générale du programme et à l'initialisation de WebGL incluant l'écriture du code des shaders. Le second article sera consacré à la boucle d'animation. Les deux articles ne rentreront pas dans le détail d'un commentaire ligne par ligne du code de l'exemple mis à disposition, mais rien de ce qui concerne WebGL ne sera ignoré.

La solution

L'expérience montre qu'en l'espèce, multiplier les appels à drawElements () pénalise beaucoup les performances. Il faut donc adopter la solution consistant à déporter dans les shaders tous les calculs requis pour transformer et rendre tous les "pixels" à l'occasion d'un unique appel à drawElements () par étape de l'animation.

Cela a deux conséquences :

Le code du VS est un peu plus compliqué. En effet, le VS ne sert plus seulement de passe-plat entre le programme principal qui transformerait les points et le FS qui afficherait les pixels comme nous l'avons vu en étudiant comment utiliser WebGL pour un rendu vectoriel : il doit transformer les points.
Le VS a besoin de toutes les données requises pour effectuer les transformations des points d'un "pixel". Toutefois, comme il n'a accès qu'aux données spécifiques au point courant (les données passées via les arguments valent pour tous les points, étant fixées avant l'unique appel à drawElements ()), il faut annexer ces données à celles de chaque point du "pixel" dans le buffer des points.

Le code JavaScript

Le programme est structuré en plusieurs parties :

l'initialisation générale assurée par run () ;
l'initialisation de l'explosion assurée par explode () ;
le rendu d'une étape de l'explosion assurée par nextStep ().

Cet article porte sur la première partie, l'initialisation générale. Un second article présentera les deux autres.

Tout d'abord, il faut créer un élément HTML canvas et d'obtenir son contexte WebGL, rajouté au document comme enfant d'un élément HTML quelconque (en l'occurrence un élément d'identifiant tagCanvas) :

var CANVAS_WIDTH = 800;
var CANVAS_HEIGHT = 600;
var canvas;
var gl;

canvas = document.createElement ("canvas");
canvas.width = CANVAS_WIDTH;
canvas.height = CANVAS_HEIGHT;
document.getElementById ("tagCanvas").appendChild (canvas);
gl = canvas.getContext ("webgl");

Noter que l'élément HTML canvas peut parfaitement avoir déjà directement mentionné dans le code HTML, auquel cas il n'est pas nécessaire pas besoin de le créer :

Ensuite, il faut créer le VS et le FS :

var shaderV, shaderF;

shaderV = gl.createShader (gl.VERTEX_SHADER);
gl.shaderSource (shaderV, "attribute vec2 A_xy; attribute vec3 A_rgb; attribute vec4 A_bzdxdy; uniform mat4 U_mW; varying lowp vec3 V_rgb; void main (void) { mat4 m; m = mat4 (1.0); m[0][0] = cos (A_bzdxdy.x) * A_bzdxdy.y; m[1][0] = - sin (A_bzdxdy.x) * A_bzdxdy.y; m[0][1] = sin (A_bzdxdy.x) * A_bzdxdy.y; m[1][1] = cos (A_bzdxdy.x) * A_bzdxdy.y; m[3][0] = A_bzdxdy.z; m[3][1] = A_bzdxdy.w; gl_Position = U_mW * m * vec4 (A_xy.xy, 0.0, 1.0); V_rgb = A_rgb; }");
gl.compileShader (shaderV);
if (!gl.getShaderParameter (shaderV, gl.COMPILE_STATUS))
	alert (gl.getShaderInfoLog (shaderV));
shaderF = gl.createShader (gl.FRAGMENT_SHADER);
gl.shaderSource (shaderF, "varying lowp vec3 V_rgb; uniform lowp float U_a; void main (void) { gl_FragColor = vec4 (V_rgb, U_a); }");
gl.compileShader (shaderF);
if (!gl.getShaderParameter (shaderF, gl.COMPILE_STATUS))
	alert (gl.getShaderInfoLog (shaderF));
program = gl.createProgram ();
gl.attachShader (program, shaderV);
gl.attachShader (program, shaderF);
gl.linkProgram (program);
gl.useProgram (program);

Enfin, il faut obtenir des références sur les attributs et les uniformes des shaders afin d'en préciser les valeurs ultérieurement :

var A_xy, A_rgb, A_bzdxdy, U_mW, U_a;

A_xy = gl.getAttribLocation (program, "A_xy");
A_rgb = gl.getAttribLocation (program, "A_rgb");
A_bzdxdy = gl.getAttribLocation (program, "A_bzdxdy");
U_mW = gl.getUniformLocation (program, "U_mW");
U_a = gl.getUniformLocation (program, "U_a");

L'exemple

Cliquez ici pour accéder à une page de test minimaliste (un simple "pixel" est affiché après l'initialisation décrite à l'instant). Vous pourrez visualiser le code et le récupérer pour travailler avec.

La logique

La création du canvas et la récupération du contexte WebGL ainsi que la récupération de références sur les attributs et les uniformes (dont le rôle sera précisé plus loin) ne prêtent pas à commentaires. Le vrai sujet est la création des shaders, et plus précisément l'écriture du code de ces derniers. Avant de plonger dans le code du VS, il faut expliquer ce qui est attendu de ce dernier.

Ce qui est attendu du VS

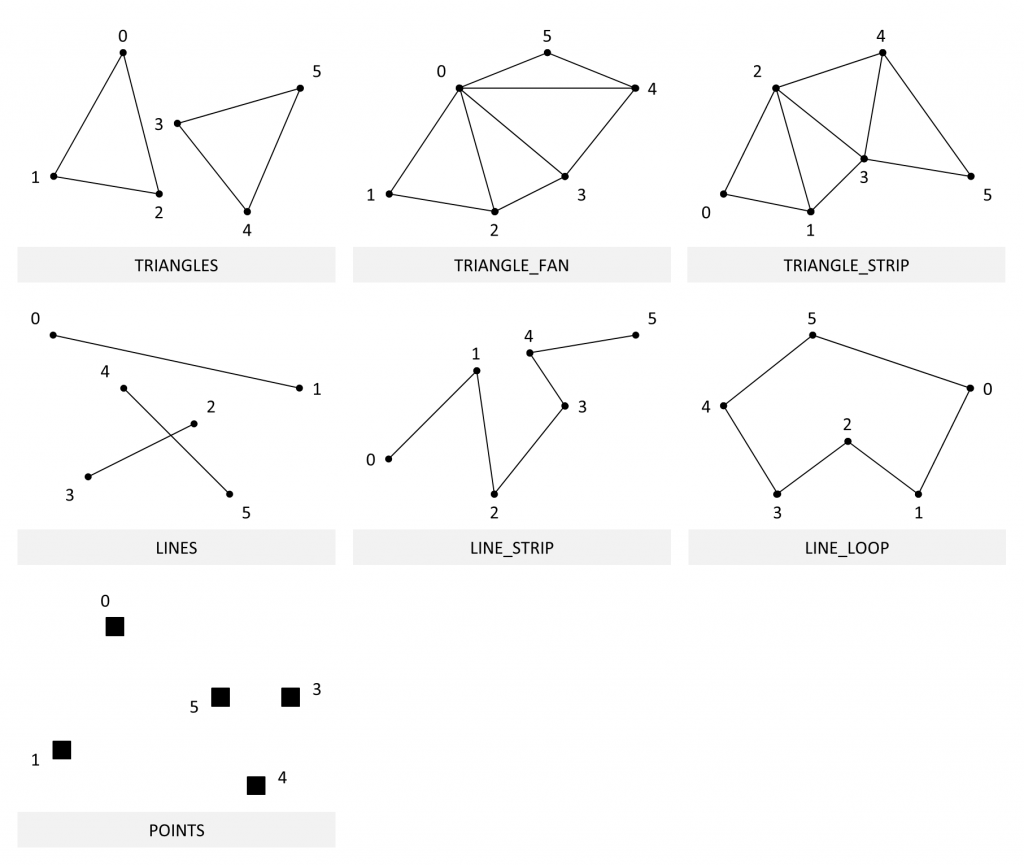
WebGL peut manipuler différents types de primitives :

En l'espèce, chaque "pixel" est représenté sous la forme de deux triangles distincts, c'est-à-dire deux primitives TRIANGLES.

A priori, ce choix n'est pas judicieux.

Pourquoi ne pas utiliser des POINTS ? Parce qu'un point n'est pas une surface, ce qui signifie qu'il est impossible de lui appliquer une transformation telle que la rotation envisagée - le zoom est possible, en jouant sur la variable système du VS gl_PointSize. Va donc pour des triangles.

Mais alors, pourquoi ne pas utiliser des TRIANGLE_STRIP ou des TRIANGLE_FAN ? En effet, ces primitives ne permettent-elles pas de décrire un "pixel" en fournissant simplement quatre points ? Utiliser TRIANGLES contraint de fournir deux fois trois points pour chaque triangle, soit six points, dont deux se répètent puisqu'ils sont communs aux deux triangles.

Certes, mais c'est inévitable et il est possible de limiter le nombre de points :

C'est inévitable, car on souhaite transformer et rendre en une seule fois tous les "pixels". Dans ces conditions, utiliser TRIANGLE_STRIP et des TRIANGLE_FAN signifie qu'il faut que WebGL permette de transformer et de rendre en une seule fois une de ces primitives par "pixel". Or WebGL ne le permet pas : c'est un TRIANGLE_STRIP ou un TRIANGLE_FAN par appel à drawArrays () ou drawElements ().
Il est possible de limiter le nombre de points, car WebGL permet de commander la transformation et le rendu via drawElements () plutôt que drawArrays (). Avec drawElements (), il suffit de fournir quatre points et six indices, trois indices consécutifs référençant les points qui forment un TRIANGLES.

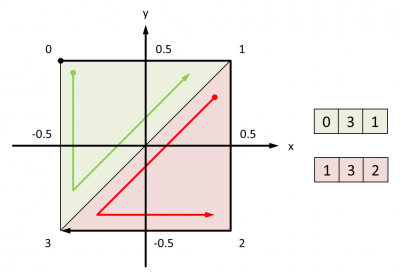
Les deux TRIANGLES sont décrits à l'aide de quatre points formant un carré de 1.0 x 1.0 centré sur (0.0, 0.0), et de deux jeux de trois indices :

Un "pixel" composé de deux TRIANGLES aux points indexés

Au passage, une bonne habitude à prendre en perspective d'un passage à la vraie 3D - l'explosion de "pixels" est en 2D - consiste à donner les points d'une surface dans l'ordre qui évite l'élimination de la surface par culling des faces arrières. Autrement dit, donner les points dans le sens trigonométrique. Pour vérifier que ce sens est respecté, il est possible d'activer le culling, par défaut désactivé :

gl.enable(gl.CULL_FACE);
gl.cullFace (gl.BACK);

Comme nous l'avons vu en étudiant comment utiliser WebGL pour un rendu vectoriel, le VS est alimenté en données relatives au point courant via des attributs. Ces données sont extraites de ARRAY_BUFFER, un buffer interne de WebGL auquel bindBuffer () permet d'associer un buffer créé avec createBuffer () et alimenté en données avec bufferData () (ou partiellement alimenté avec bufferSubData (), comme il en sera question dans le second article) :

var vertices = [
	-0.5,	0.5,	1.0,	0.0,	0.0,
	0.5,	0.5,	1.0,	0.0,	0.0,
	0.5,	-0.5,	1.0,	0.0,	0.0,
	-0.5,	-0.5,	1.0,	0.0,	0.0,
];
var bufferV;

bufferV = gl.createBuffer ();
gl.bindBuffer (gl.ARRAY_BUFFER, bufferV);
gl.bufferData (gl.ARRAY_BUFFER, new Float32Array (vertices), gl.STATIC_DRAW);

Choix a été fait d'utiliser des indices en plus des points. Comme les points, les indices doivent être fournis sous la forme d'un tableau qui sert à alimenter un autre buffer, pour sa part associé au buffer interne de WebGL ELEMENT_ARRAY_BUFFER :

var indices = [
	0, 3, 1,
	1, 3, 2
];
var bufferI;

bufferI = gl.createBuffer ();
gl.bindBuffer (gl.ELEMENT_ARRAY_BUFFER, bufferI);
gl.bufferData (gl.ELEMENT_ARRAY_BUFFER, new Uint16Array (indices), gl.STATIC_DRAW);

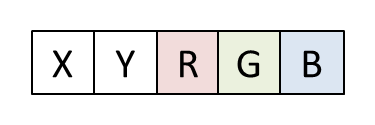
Retour aux points. Un point se présente sous la forme d'une série de nombres décimaux respectant un format de point dont la définition implicite est libre. En l'espèce, le format de point est le suivant :

Toutefois, l'abscisse, l'ordonnée et la couleur d'un point ne sont pas les seules données dont le VS a besoin pour effectuer le travail attendu de lui. En effet, on souhaite qu'il transforme ce point en lui appliquant une rotation, puis un zoom, puis une translation. La particularité est que ces transformations sont identiques pour les quatre points des deux TRIANGLES composant un "pixel". Comment le VS peut-il accéder à l'angle β, au facteur de zoom Z et aux composantes du vecteur de translation dX et dY propre au "pixel" courant ? Et d'abord, comment pourrait-il deviner à quel "pixel" le point courant appartient ?

La réponse est simple : le VS ne peut pas savoir à quel "pixel" le point courant appartient. Il travaille au niveau du point, pas de la primitive, et encore moins de l'objet dont cette dernière relève dans le programme principal - le fameux "pixel". Par conséquent, dans un contexte où le VS va être appelé en rafale pour transformer tous les points de tous les "pixels" en une fois, si donnée supplémentaire il faut lui transmettre, il faut lui transmettre via :

une uniforme si jamais cette donnée est la même pour tous les points qu'il doit traiter ;
un attribut - donc via ARRAY_BUFFER - si jamais cette donnée est propre au point courant.

Bref, β, Z, dX et dY doivent être rajoutées dans ARRAY_BUFFER.

L'organisation des données

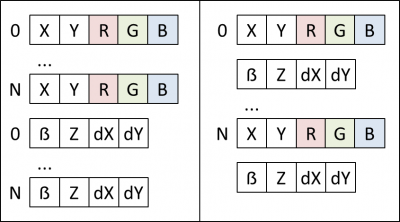
Deux schémas peuvent être envisagés pour intégrer β, Z, dX et dY à ARRAY_BUFFER. Dans le premier schéma (à gauche), ces données sont rajoutées après les données des points, alors que dans le second (à droite), elles sont rajoutées après les données de chaque point :

Le choix du schéma peut constituer un enjeu pour les performances. Du fait qu'il vaut mieux regrouper les données qui n'ont pas besoin d'être modifiées durant l'animation, d'une part, et les données qui ont besoin d'être modifiées durant l'animation, d'autre part, on opte ici pour le premier schéma - le second article de cette série reviendra là-dessus.

Le contenu de ARRAY_BUFFER ainsi organisé, il faut porter cette organisation à la connaissance du VS. Comme le format de point, cela se fait de manière implicite en définissant des attributs qui sont alimentés avec les bonnes données :

A_xy de type vec2 pour X et Y (accessibles via A_xy.x et A_xy.y dans le code du VS, respectivement) ;
A_rgb de type vec3 pour R, G et B (accessibles via A_rgb.x, A_rgb.y et A_rgb.z dans le code du VS, respectivement) ;
A_bzdxdy de type vec4 pour β, Z, dX et dY (accessibles via A_bzdxdy.x, A_bzdxdy.y, A_bzdxdy.z, A_bzdxdy.w dans le code du VS, respectivement).

Ces attributs doivent être déclarés dans le code du VS et associés à ARRAY_BUFFER dans le programme principal. Dans le code du VS, ils sont simplement déclarés avant main () :

attribute vec2 A_xy;
attribute vec3 A_rgb;
attribute vec4 A_bzdxdy;

Dans le programme principal, une fois les shaders compilés et rattachés à un programme compilé, ils sont associés à des variables par getAttribLocation () (une variable du programme principal ne doit pas nécessairement prendre le nom de la variable du shader à laquelle elle est associée, mais c'est plus pratique pour s'y retrouver) :

var A_xy, A_rgb, A_bzdxdy;

A_xy = gl.getAttribLocation (program, "A_xy");
A_rgb = gl.getAttribLocation (program, "A_rgb");
A_bzdxdy = gl.getAttribLocation (program, "A_bzdxdy");

Ces variables sont ensuite associées à ARRAY_BUFFER via vertexAttribPointer (), mais il en sera question dans le second article de cette série.

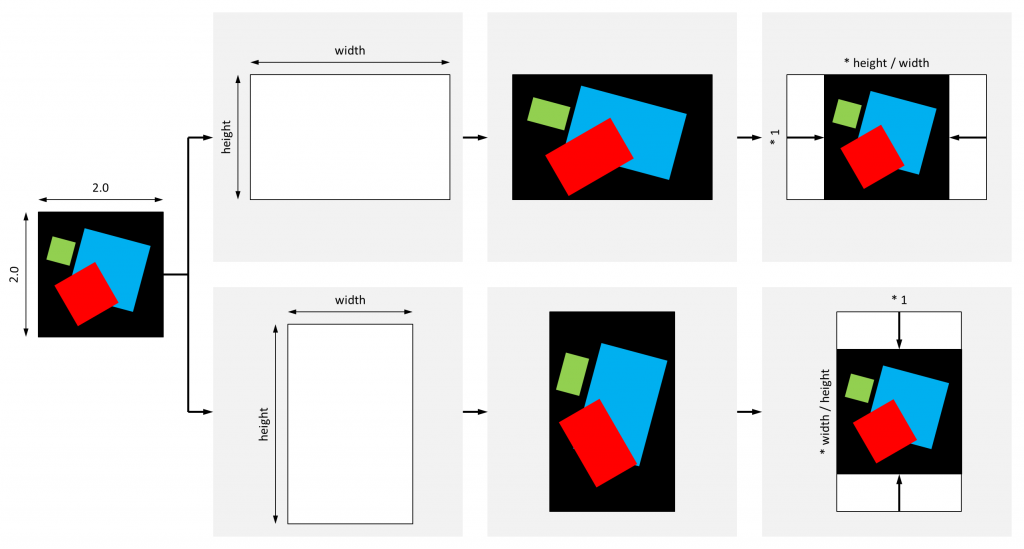
Pour alimenter le VS, il ne reste plus qu'à lui transmettre une matrice de transformation générale qui s'applique à tous les "pixels". Cette matrice sert pour ajuster l'aspect ratio, c'est-à-dire pour s'assurer que la projection d'un pixel carré dans l'espace sera bien carrée à l'écran, quand bien même la surface du canvas que WebGL considère correspondre à une surface de 2.0 x 2.0 dans l'espace n'est pas carrée. Par exemple, à l'occasion d'un rendu dans un canvas de 800x400, le rendu sans ajustement de l'aspect ratio en haut et avec ajustement de l'aspect ratio en bas :

Il convient donc de corriger les coordonnées des points d'un facteur qui dépend de la situation pour restituer l'espace à l'écran sans déformation :

La matrice permet aussi d'appliquer une transformation identique à tous les "pixels", en l'occurrence leur appliquer une rotation autour du centre de l'écran. Une fonction getWorldMatrix () renvoie cette matrice :

function getWorldMatrix (angle, zoom, width, height) {
	var mWorld;

	zoom = 1.0;
	width = CANVAS_WIDTH;
	height = CANVAS_HEIGHT;
	mWorld = [
		Math.cos (angle), Math.sin (angle), 0.0, 0.0,
		- Math.sin (angle), Math.cos (angle), 0.0, 0.0,
		0.0, 0.0, 1.0, 0.0,
		0.0, 0.0, 0.0, 1.0
	];
	if (width > height) {
		mWorld[0] *= height * zoom / width;
		mWorld[1] *= zoom;
		mWorld[4] *= height * zoom / width;
		mWorld[5] *= zoom;
	}
	else {
		mWorld[0] *= zoom;
		mWorld[1] *= width * zoom / height;
		mWorld[4] *= zoom;
		mWorld[5] *= width * zoom / height;
	}
	return (mWorld);
}

S'agissant d'une donnée identique pour tous les points transformés, la matrice peut être transmise au VS via une uniforme, en l'occurence U_mW. Comme les attributs, cette uniforme est déclarée avant main () dans le VS :

uniform mat4 U_mW;

Dans le programme principal, U_mW est accédée par l'intermédiaire d'une variable associée par getUniformLocation () :

U_mW = gl.getUniformLocation (program, "U_mW");

De la même manière, une uniforme U_a correspondant au degré de transparence, l'alpha, est définie dans le VS et associée à une variable U_a dans le programme principal. En effet, l'alpha est le même pour tous les "pixels" qui disparaîtront de l'écran à la même vitesse tandis que cet alpha passera de 1.0 (opacité totale) à 0.0 (transparence totale).

Le code du VS

Mis à plat, le code du VS est le suivant :

attribute vec2 A_xy;
attribute vec3 A_rgb;
attribute vec4 A_bzdxdy;
uniform mat4 U_mW;
varying lowp vec3 V_rgb;

void main (void) {
	mat4 m;

	m = mat4 (1.0);
	m[0][0] = cos (A_bzdxdy.x) * A_bzdxdy.y;
	m[1][0] = - sin (A_bzdxdy.x) * A_bzdxdy.y;
	m[0][1] = sin (A_bzdxdy.x) * A_bzdxdy.y;
	m[1][1] = cos (A_bzdxdy.x) * A_bzdxdy.y;
	m[3][0] = A_bzdxdy.z;
	m[3][1] = A_bzdxdy.w;
	gl_Position = U_mW * m * vec4 (A_xy.xy, 0.0, 1.0);
	V_rgb = A_rgb;
}

Ce code est très simple, car il n'effectue qu'une multiplication de matrices : une matrice de transformation m propre au "pixel" - donc au point - est multipliée par la matrice des coordonnées du point, puis la matrice de transformation générale U_mW est multipliée au résultat. Autrement dit, le point est d'abord transformé localement puis globalement, comme il se doit.

A ce point, il convient de faire un aparté sur les matrices. L'usage des matrices dans un shader est particulièrement contre-intuitif pour qui a appris à en adresser les éléments en ligne puis en colonne. En effet, dans une variable de type matrice d'un shader, les éléments s'adressent en colonne puis en ligne :

mat4 m;

m[2][3] = 100.0; // L'élément figurant à la 3ème colonne ([2]) de la 4ème ligne ([3]) passe à 100.0

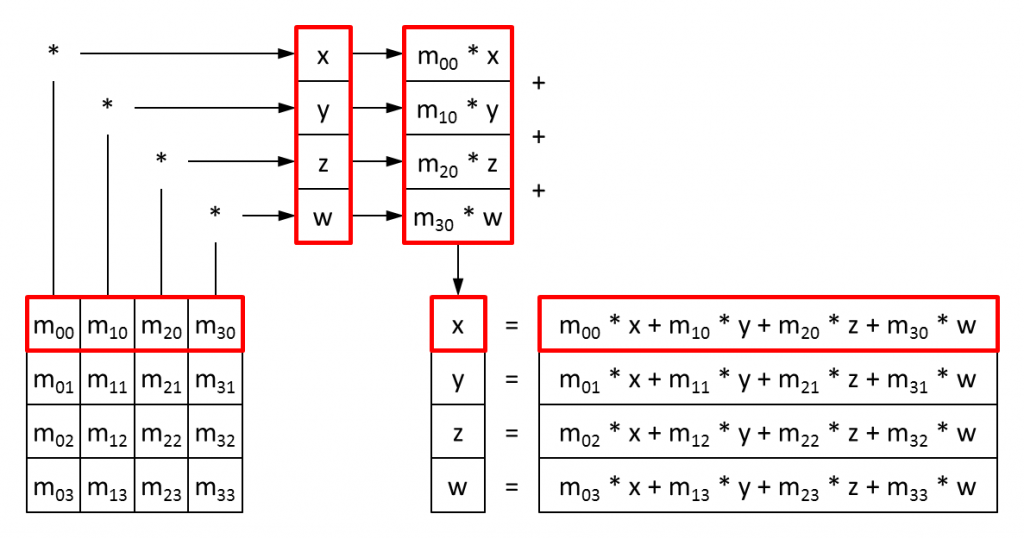
Bref, il faut se représenter l'opération consistant à multiplier m par vec4 (A_xy.xy, 0.0, 1.0) ainsi (les éléments étant numérotés en donnant la colonne puis la ligne) :

Multiplication d'une matrice et d'un vecteur

Dans le code du shader, la multiplication de la matrice mat4 m par un vecteur vec4 v s'écrit m * v, et non l'inverse.

Attention ! Dans le programme principal en JavaScript, l'alimentation d'une uniforme de type mat4 par un tableau de valeurs se fait en colonne :

var m = [
	m00, m01, m02, m03,
	m10, m11, m12, m13,
	m20, m21, m22, m23,
	m30, m31, m32, m33
];
var U_m = gl.getUniformLocation (program, "U_m");
gl.uniformMatrix4fv (U_m, false, m);

Noter que l'argument de transposition doit toujours être false, car la transposition ne marche pas.

Retour à la transformation d'un point d'un "pixel". Nous avons déjà vu comment appliquer une rotation à un point autour d'un centre. Toutefois, c'était dans un repère dont l'axe des abscisses est orienté de gauche à droite et l'axe des ordonnées est orienté de haut en bas. Dans le contexte de WebGL, l'axe des abscisses est pareillement orienté, mais l'axe des ordonnées est orienté à l'inverse, de bas en haut. Par conséquent, appliquer à un point A une rotation d'angle β autour d'un centre O produit un point B tel que :

x_B = x_O + (x_A - x_O) * cos (β) - (y_A - y_O) * sin (β)
y_B = y_O + (y_A - y_O) * sin (β) + (y_A - y_O) * cos (β)

La rotation doit être combinée au zoom, les deux se déroulant simultanément. Enfin, la translation peut être effectuée. C'est l'ordre dans lequel les transformations se déroulent quand elles sont décrites par une matrice multipliée à celle qui contient les coordonnées du point :

`m[0][0]`	Z * cos (β)	`m[1][0]`	- Z * sin (β)	`m[2][0]`	0	`m[3][0]`	dX
`m[0][1]`	Z * sin (β)	`m[1][1]`	Z * cos (β)	`m[2][1]`	0	`m[3][1]`	dY
`m[0][2]`	0	`m[1][2]`	0	`m[2][2]`	1	`m[3][2]`	0
`m[0][3]`	0	`m[1][3]`	0	`m[2][3]`	0	`m[3][3]`	1

Cette matrice est assemblée dans le code du VS, récupérant β, Z, dX et dY dans l'attribut via lequel elles parviennent :

`β`	`A_bzdxdy.x`
`Z`	`A_bzdxdy.y`
`dX`	`A_bzdxdy.z`
`dY`	`A_bzdxdy.w`

Au terme de ses calculs, le VS doit livrer deux données qui intéressent le FS. En effet, le FS doit déterminer les pixels que la projection du TRIANGLES occupe à l'écran puis les colorier en interpolant les couleurs des sommets de ce TRIANGLES. Le VS doit donc livrer :

Les coordonnées transformées du point. Pour cela, le VS doit alimenter la variable système gl_Position. S'agissant d'une variable système, elle n'a pas à être déclarée.
La couleur du point. Pour cela, le VS doit alimenter une variante, une variable dont le type indique au FS qu'il doit en déterminer la valeur pour le pixel courant en interpolant les valeurs qu'elle prend aux sommets du TRIANGLES. Cette variable V_rgb est déclarée avant main (), tant dans le code du VS que dans le code FS pour faire le lien.

Ce qui conduit à aborder le code du FS.

Le code du FS

Mis à plat, le code du FS est le suivant :

varying lowp vec3 V_rgb;
uniform lowp float U_a;

void main (void) {
	gl_FragColor = vec4 (V_rgb, U_a);
}

Ce code est totalement trivial, puisqu'il consiste à demander au FS d'afficher un pixel dont la couleur est celle résultant de l'interpolation déjà évoquée, sans plus. Pour cela, le FS doit alimenter une variable système gl_FragColor.

L'initialisation est terminée. Il ne reste plus qu'à animer...

Stash of Code

Bits of help for writing code

Menu

Shader d’explosion de pixels avec WebGL (1/2)

La solution

Le code JavaScript

L'exemple

La logique