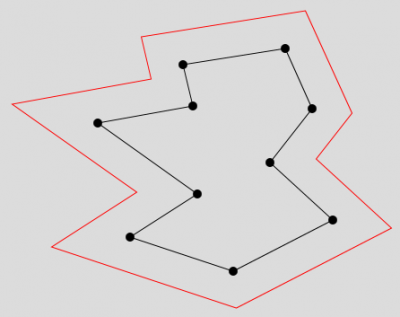
Comment déterminer les coordonnées de la normale en un angle d'un polygone ? En disposer est très utile pour appliquer une déformation homothétique au polygone. En effet, c'est est le long de ces normales qu'il est possible de déplacer les sommets du polygone pour produire des versions de ce dernier parfaitement emboîtées (enveloppes homothétiques) :
La solution
La solution est toute mathématique. Elle consiste à calculer la version normalisée de la somme des normales aux côtés qui forment l'angle, en veillant à l'orientation de ces normales qui dépend du choix du sens de rotation (par défaut, trigonométrique).
Le code JavaScript
En JavaScript, la solution se traduit par le code suivant :
/*------------------------------------------------------------------------------
Retourne la normale en un angle.
ENTREE :
A Point A
B Point B (où la normale est calculée)
C Point C
SORTIE :
Coordonnées de la normale au point B (les coordonnées ne sont pas entières).
------------------------------------------------------------------------------*/
function angleNormal (A, B, C) {
var BM = Math.sqrt (Math.pow (C.y - A.y, 2) + Math.pow (A.x - C.x, 2));
var xM = B.x + (C.y - A.y) / BM;
var yM = B.y + (A.x - C.x) / BM;
return ({x:xM, y:yM});
}
L'exemple
Cliquez ici pour accéder à une page de test minimaliste. Vous pourrez visualiser le code et le récupérer pour travailler avec.
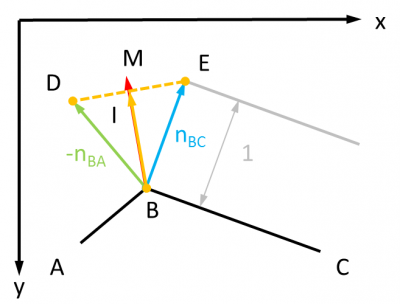
Les maths
La normale recherchée est une version normalisée (ie : sa distance est rapportée à 1) de la somme des deux normales aux côtés du polygone qui forment l'angle.
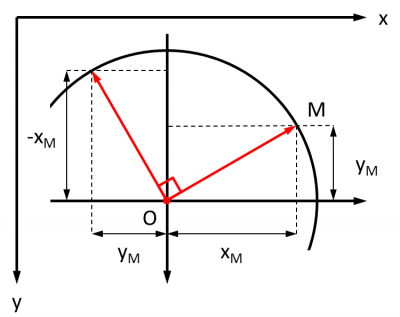
Les coordonnées d'une normale à un côté se calculent facilement, comme il est possible de le constater avec un exemple dans le cercle trigonométrique :
C'est ainsi que se calculent les coordonnées de nAB et nBC. Par exemple, pour nBC, on sait que :
- xBC = (xC - xB) / BC
- yBC = (yC - yB) / BC
Donc :
- xnBC = (yC - yB) / BC
- ynBC = (xB - xC) / BC
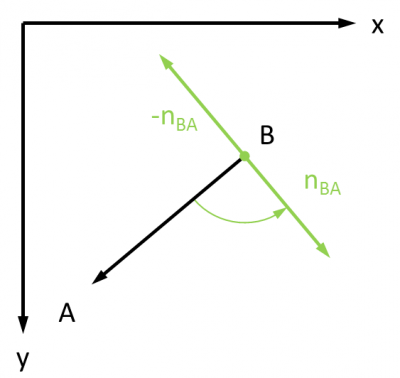
Pour nBA, le raisonnement est identique, mais du fait du sens de rotation trigonométrique adopté, il faut calculer la version symétrique la normale par rapport à B, ce qui revient à inverser les signes de l'abscisse et de l'ordonnée :
Ce qui donne :
- xnBA = (yB - yA) / AB
- ynBA = (xA - xB) / AB
Comme xnBA = xB - xD :
- xD = xB + (yB - yA) / AB
- yD = yB + (xA - xB) / AB
Et comme xnBC = xE - xD :
- xE = xB + (xC - xB) / BC
- yE = yB + (xB - xC) / BC
Maintenant, les coordonnées de I, centre de DE :
- xI = (xD + xE) / 2
- yI = (yD + yE) / 2
La normale et le vecteur BI sont colinéaires, donc :
- xBM = (xI - xB) / IB
- yBM = (yI - yB) / IB
Et comme xBM = xM - xB et yBM = yM - yB :
- xM = xB + (xI - xB) / IB
- yM = yB + (yI - yB) / IB
Attention ! L'ordre des points importe dans l'appel à
angleNormal () ! Inverser A et C conduit à calculer la normale inverse, c'est-à-dire une normale qui semblerait rentrer dans le polygone plutôt que d'en sortir.