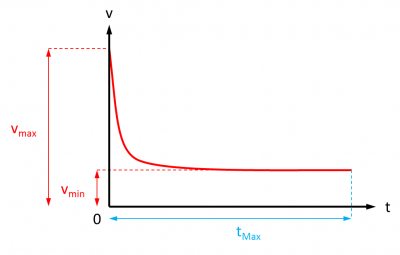
Comment produire un effet de ralentissement du mouvement réaliste ? La solution qui vient spontanément à l'esprit n'est pas réaliste : elle consiste à faire décroître la vitesse du mouvement de manière linéaire. Dans la réalité, le ralentissement est très fort au début et très faible à sa fin, donnant l'impression d'un amortissement :
La solution
Entre l'instant où le freinage débute et l'instant où il se termine, la vitesse doit passer d'un maximum à un minimum selon une loi de décroissance en 1/t2, t étant le temps écoulé.
Le code JavaScript
En JavaScript, la solution se traduit par le code suivant :
/*------------------------------------------------------------------------------
Retourne la valeur correspondant à l'étape n sur de l'interpolation en 1/R² d'une valeur entre un minimum (à l'étape 1) et un maximum (à l'étape N).
ENTREE
min Valeur minimale
max Valeur maximale
nbSteps Nombre d'étapes de l'interpolation
n Etape de l'interpolation
xMax Abscisse maximale de la portion de 1/x² utilisée
xMin Abscisse minimale de la portion de 1/x² utilisée
doRound Arrondir la valeur retournée
SORTIE
La valeur interpolée à l'étape n.
-----------------------------------------------------------------------------*/
function interpolateInverseSquare (min, max, nbSteps, step, xMin, xMax, doRound) {
var x, xM, alpha;
xM = xMin + (xMax - xMin) * step / nbSteps;
alpha = 1.0 / (xMin * xMin) - 1.0 / (xM * xM);
return (min + (max - min) * alpha / (1.0 / (xMin * xMin) - 1.0 / (xMax * xMax)));
if (doRound)
return (Math.round (x));
else
return (x);
}
L'exemple
Cliquez ici pour accéder à une page de test minimaliste. Vous pourrez visualiser le code et le récupérer pour travailler avec.
Les maths
A l'instar de la loi normale, la loi en carré inverse est une de ces lois qui gouvernent bien des phénomènes qui nous entourent, au point de rendre bizarre toute tentative de simulation de ces derniers qui ne s'y plie pas. Sans doute sommes-nous capables de détecter sans effort des ralentissements selon la loi en carré inverse à force d'y être confrontés et de chercher à agir en anticipant leur déroulement pour survivre, mais c'est un vaste débat...
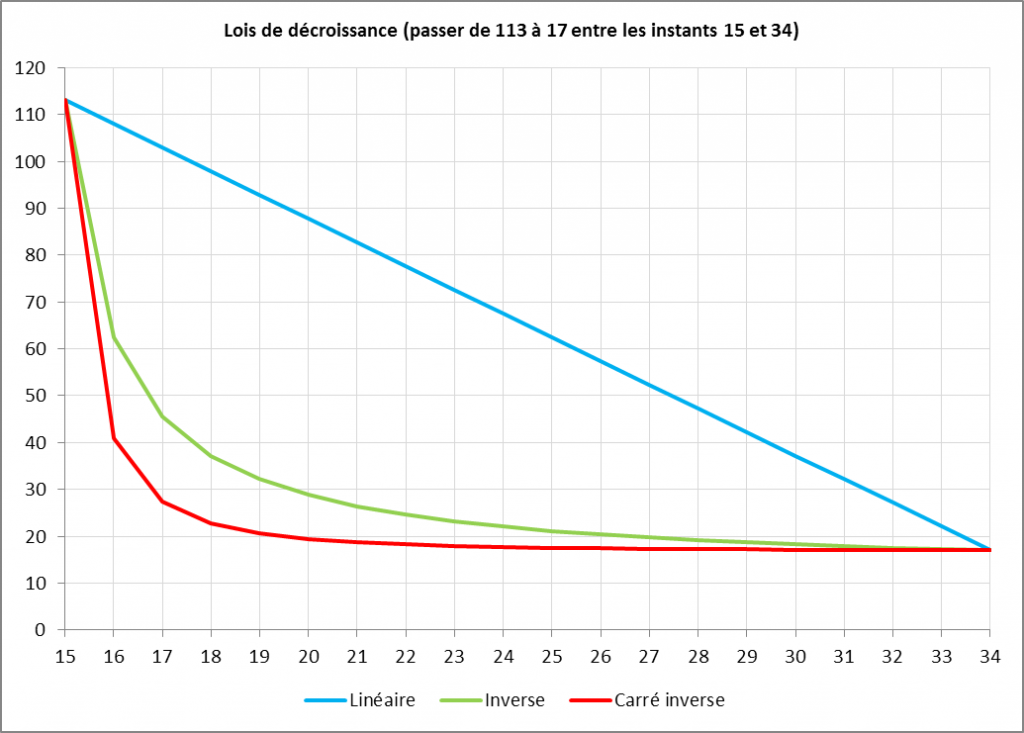
La loi en carré inverse permet de faire évoluer une valeur entre des valeurs minimale et maximale, par exemple entre 113 et 17, en un certain nombre d'étapes, par exemple 20 (numérotées de 15 à 34), selon un courbe qui accuse une décroissance très rapide (dans l'exemple, la valeur 40 est atteinte dès la 2ème étape) :
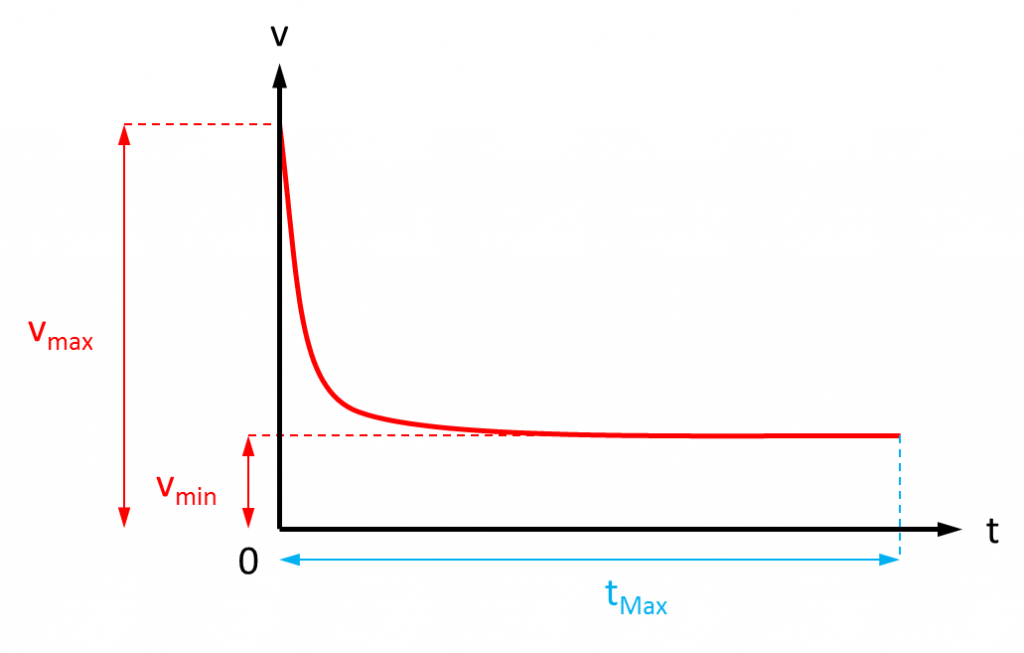
L'objectif est de parvenir à une représentation semblable, où un valeur v passe de vmax à vmin entre t = 0 et t = tmax selon une décroissance en 1/t2:
La courbe de 1/t2 ne se prête pas à ce calcul, car la valeur en 0 est infinie ; elle ne peut être rapportée à vmax. Il faut donc utiliser une astuce, qui consiste à n'utiliser qu'une partie de la courbe correspondant à un intervalle [xmin, xmax] où elle est définie :
Le choix de l'intervalle détermine la nature du ralentissement. Plus xmin est petit, plus le ralentissement est brutal au démarrage. Plus xmax est grand, plus le ralentissement s'étend en longueur à la fin. Il n'y pas pas de règle pour définir l'intervalle idéal, sinon en juger empiriquement.
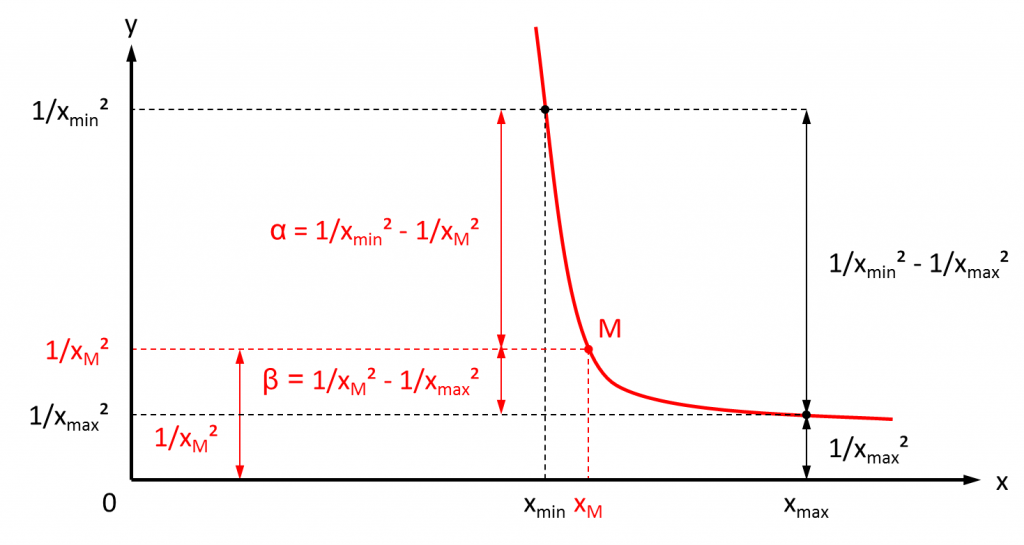
Si l'interpolation doit permettre de passer de vmax à vmin en nbSteps étapes, le calcul de v à l'étape step (compris entre 1 et nbSteps) implique tout d'abord de rapporter step à une valeur de x. Cela s'effectue via une règle de trois et un décalage (il s'agit de rapporter une valeur step de [1, nbSteps] à une valeur xM de [xmin, xmax] :
xM = xMin + (xMax - xMin) * step / nbSteps
Ensuite, il convient de calculer la valeur de y correspondant à la valeur de v recherchée. Sur le graphique précédent, deux quantités α et β sont représentées. Leurs valeurs sont déduites des valeurs de y correspondant à xmin (ie : 1 / xmax2) et xmax (ie : 1 / xmin2) :
- α = 1 / xmin2 - 1 / xM2
- β = 1 / xM2 - 1 / xmax2
α décroît et β croît tandis que x croît.
Ayant choisi une de ces quantité, il ne reste plus qu'à rapporter sa valeur à une valeur de v. Ici encore, cela s'effectue via une règle de trois et un décalage (il s'agit de rapporter une valeur y de [1 / xmax2, 1 / xmin2] à v de [vmin, vmax]) :
- α = vmin + (vmax - vmin) * α / (1 / xmin2 - 1 / xmax2)
- β = vmin + (vmax - vmin) * β / (1 / xmin2 - 1 / xmax2)
Disposer d'une telle fonction peut s'avérer utile en 3D pour neutraliser l'effet du changement de profondeur. En effet, en 3D, quand la distance à l'observateur d'une surface S est multipliée par n, l'aire de la projection de S est divisée par le carré de ce facteur, soit quatre. On démontre facilement la généralité d'une décroissance en 1/R2 de la surface :
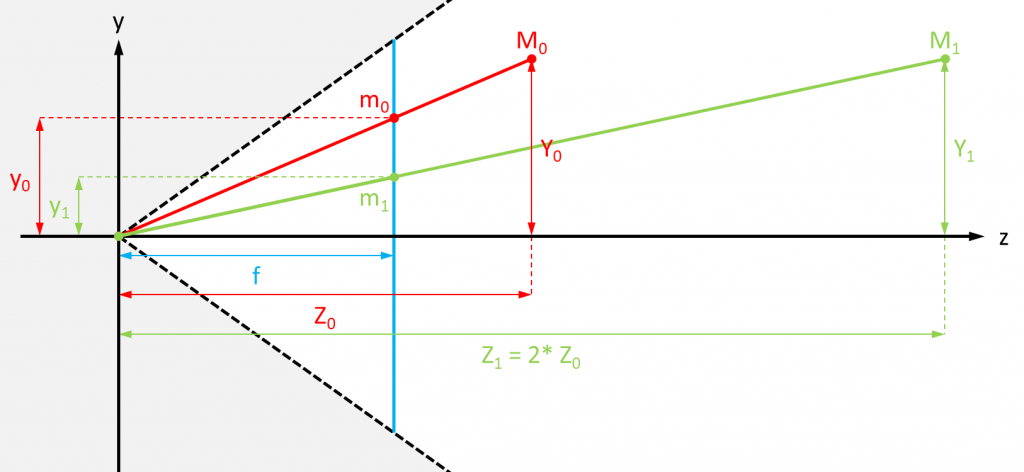
En appliquant le théorème de Thalès, on calcule les coordonnées (x0, y0) de M0, projection du point M0 (X0, Y0, Z0) sur la surface de projection (ie : l'écran) quand la distance focale est f (généralement, l'origine du repère est placée non pas à la position de l'observateur, mais sur le plan de projection ; ce n'est pas grave) :
- x0 = X0 * f / Z0
- y0 = Y0 * f / Z0
Si le point M0 est repoussé en M1 où sa distance à l'observateur est double, les coordonnées de la projection M1 de M1 (X0, Y0, 2 * Z0) sont :
- x1 = X0 * f / (2 * Z0)
- y1 = Y0 * f / (2 * Z0)
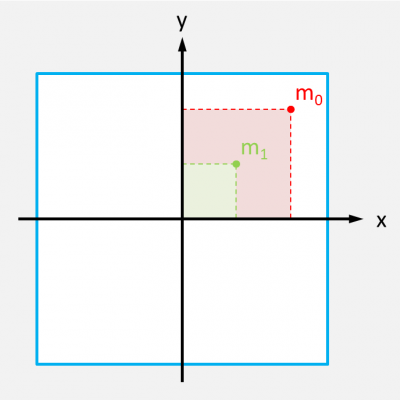
Chaque projection d'un point détermine un surface à l'origine dans la surface de projection.
Le calcul d'aire montre que la surface S1 est quatre fois plus petite que la surface S0 :
- S0 = x0 * y0 = X0 * Y0 * f2 / Z02
- S1 = x1 * y1 = X0 * Y0 * f2 / (4 * Z02) = S0 / 22